- 直线的倾斜角与斜率
- 共186题
如图,在直三棱柱ABC﹣A1BlC1中,AC=BC=
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面B1CD:
(3)求异面直线AC1与B1C所成角的余弦值。
正确答案
见解析。
解析
(1)证明:∵CC1⊥平面ABC,AC⊂平面ABC,∠ACB=90°,
∴CC1⊥AC,AC⊥BC,又BC∩CC1=C,
∴AC⊥平面BCC1,BC1⊂平面BCC1,
∴AC⊥BC1。
(2)
如图,设CB1∩C1B=E,连接DE,
∵D为AB的中点,E为C1B的中点,∴DE∥AC1,
∵DE⊂平面B1CD,AC1⊄平面B1CD,
∴AC1∥平面B1CD。
(3)由DE∥AC1,∠CED为AC1与B1C所成的角,
在△CDE中,DE=


CE=




cos∠CED=


∴异面直线AC1与B1C所成角的余弦值为
知识点
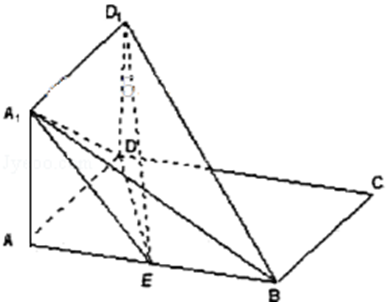
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点。
(1)求证:BD1∥平面A1DE
(2)求证:D1E⊥A1D;
(3)求点B到平面A1DE的距离。
正确答案
见解析。
解析
(1)证明:∵正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点,设O为AD1的中点,
则由三角形的中位线性质可得OE∥BD1。
由于OE⊂平面A1DE,BD1不在平面A1DE内,故BD1∥平面A1DE。
(2)证明:由题意可得D1A 是D1E在平面AA1D1D内的射影,由正方形的性质可得D1A⊥A1D,
由三垂线定理可得D1E⊥A1D。
(3)设点B到平面A1DE的距离为h,由于线段AB和平面A1DE交于点E,且E为AB的中点,
故A、B两点到平面A1DE的距离相等,即求点A到平面A1DE的距离h。
由于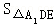


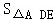
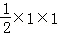
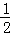
∵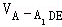
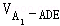
∴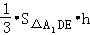

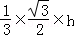
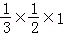
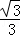
知识点
如图,在四棱锥E—ABCD中,底面ABCD为正方形,AE


(1)若F为DE的中点,求证:BE//平面ACF;
(2)求直线BE与平面ABCD所成角的正弦值。
正确答案
见解析
解析
(1)连结











(2)过
























由



又





知识点
如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AD点F是棱PD的中点,点E为CD的中点。
(1)证明:EF∥平面PAC;
(2)证明:PE⊥AF;
(3)求二面角B﹣PC﹣D的大小。
正确答案
见解析。
解析
(1)∵点E,F分别为CD,PD的中点,∴EF∥PC。
∵PC⊂平面PAC,EF⊄平面PAC,
∴EF∥平面PAC。
(2)证明:∵PA⊥平面ABCD,CD⊂平面ABCD
又ABCD是矩形,∴CD⊥AD,
∵PA∩AD=A,∴CD⊥平面PAD。
∵AF⊂平面PAD,∴AF⊥CD。
∵PA=AD,点F是PD的中
又CD∩PD=D,∴AF⊥平面PDC。
∵PE⊂平面PDC,∴PE⊥AF。
(3)
过点B作BH⊥PC于H,连接DH
∵△PBC≌△PDC,∴DH⊥PC
∴∠BHD是二面角B﹣PC﹣D的二面角。
设PA=AD=1,在△BHD中,BH=DH=
∴cos∠BHD=

∴二面角B﹣PC﹣D的大小为120°。
知识点
如图,矩形














(1)求证:
(2)求异面直线MD与FC所成的角的大小
正确答案
见解析
解析
解析:
(1)证明:连接

因为平面


所以 


所以 

又 


所以 

所以 
(2)60
知识点
扫码查看完整答案与解析