直线的倾斜角与斜率
共186题

· 直线的倾斜角与斜率

直线的倾斜角与斜率
共186题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知直线2x+y-c=0与圆x2+y2=R2交于A，B两点，则与（O为坐标原点）共线的向量是

A（2,1）

B（－2,－ 4）

C（4,2）

D（－1,2）

正确答案

解析

略

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 12 分

在四棱锥中，底面ABCD是矩形，平面PAD⊥平面ABCD，PD⊥PB，。

（1）求证： PD⊥平面PAB；

（2）设E是棱AB的中点，，，

求四棱锥的体积。

正确答案

见解析

解析

（1）证明：因为平面PAD⊥平面ABCD，平面PAD平面ABCD，

所以平面PAD

又平面PAD，所以PD⊥AB

又PD⊥PB，所以PD⊥平面PAB

（2）设，则

在Rt△PAE中，

在Rt△BEC中，

由得，即，解得

所以四棱锥的高

故四棱锥的体积

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 10 分

如图，已知AB为圆O的一条直径，以端点B为圆心的圆交直线AB于C、D两点，交圆O于E、F两点，过点D作垂直于AD的直线，交直线AF于H点。

（1）求证：、、、四点共圆；

（2）若AC=2，AF=2 ,求外接圆的半径。

正确答案

见解析

解析

解析：（1）因为为圆一条直径，所以，…………2分

又，

故、、、四点在以为直径的圆上

所以，、、、四点共圆。……………4分

（2）因为与圆相切于点，由切割线定理得

,即，

，………………6分

所以

又,

则, 得……………8分

连接,由（1）可知为的外接圆直径

,故的外接圆半径为……………10分

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 12 分

已知斜三棱柱ABC－A1 B1C1，所有棱长均为2，若点A1在底面ABC的射影落在AB的中点上。

（1）在线段A1C1上找到一点N，使得MN∥面B1C1CB，求A1iN的长度；

（2）求四棱锥体积VA—BB1C1C。

正确答案

见解析

解析

（1）点为中点，。

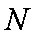
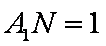
理由如下：取中点为,连结则四边形平行四边形，所以有MN即MN∥面B1 C1 CB。

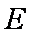
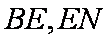
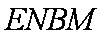
（2）=

知识点

直线的倾斜角与斜率

题型：单选题

单选题 · 5 分

一个小组的3个学生在分发数学作业时，从他们3人的作业中各随机地取出2份作业，则每个学生拿的都不是自己作业的概率是

正确答案

解析

略

知识点

直线的倾斜角与斜率

继续学习学习下一知识点

下一知识点 : 三点共线问题

百度题库 > 高考 > 文科数学 > 直线的倾斜角与斜率

扫码查看完整答案与解析