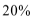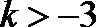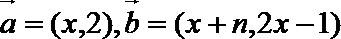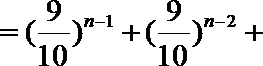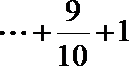- 数列与函数的综合
- 共73题
21.设
(1)求实数a;
(2)求数列{xn}的通项公式;
(3)若
正确答案
(1)由
解析
解析已在路上飞奔,马上就到!
知识点
4.已知当x∈R时,函数y=f(x)满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.政府决定用“对社会的有效贡献率”对企业进行评价用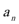
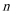
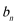

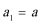
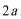
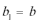
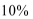

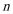
(1)求该企业第一年和第二年的“对社会的有效贡献率”;
(2)试问:从第几年起该企业“对社会的有效贡献率”不低于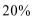
正确答案
(1)因为 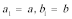
根据题意: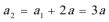

所以 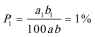

该企业第一年和第二年的“对社会的有效贡献率”分别为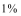
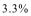
(2)因为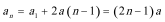
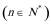
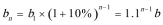
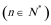
所以 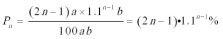
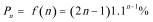
证法1: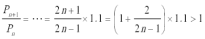
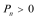
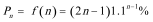
证法2: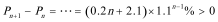

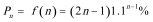
再验证: 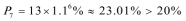
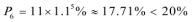
故,从第七年起该企业“对社会的有效贡献率”不低于
解析
解析已在路上飞奔,马上就到!
知识点
15.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列{an}的前n项和


(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有

(III)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.各项均为正数的等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列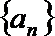
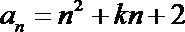
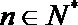
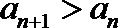
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设向量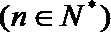
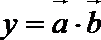
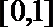
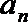
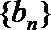
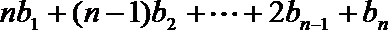
(1)求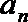
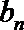
(2)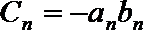
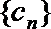
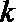
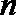
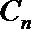
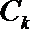
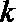
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析