- 数列与函数的综合
- 共73题
7.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.有三种卡片分别写有数字1,10和100。设m为正整数,从上述三种卡片中选取若干张,使得这些卡片上的数字之和为m。考虑不同的选法种数,例如当m=11时,有如下两种选法:“一张卡片写有1,另一张卡片写有10”或“11张写有1的卡片”,则选法种数为2。
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an 当n≥2时,求数列{an}的通项公式。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数

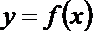
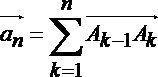
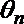
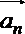
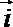
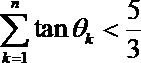
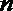
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在数列{an}中,an+1=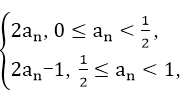

正确答案
解析
∵a1=









知识点
9.若数列 的通项公式为
正确答案
解析
令
an=7t2-3t=
当n=1时,t=1,离t0= 
故a1最大;
当n=6 时, 

故a6最小.
知识点
9.若数列


正确答案
解析
令
an=7t2-3t=
当n=1时,t=1,离t0= 
故a1最大;
当n=6 时, 

故a6最小.
知识点
19.已知函数


(1)求证:数列
(2)令




正确答案
(1)证明:由题意得
又 ∵
∴
故数列{bn + 1}是以1为首项,2为公比的等比数列
(2) 由 (1)可知,
故
∴
解析
解析已在路上飞奔,马上就到!
知识点
7.设曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
9. 已知


正确答案
解析
由


考查方向
本题主要考查了数列的函数特性,高考中数列常考的还是等差、等比数列基本公式、基本量的计算问题。
解题思路
由数列递增定义可得

易错点
本题易忽略数列是特殊函数,即定义域。
知识点
扫码查看完整答案与解析






























