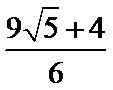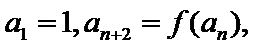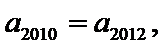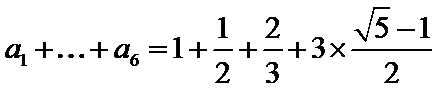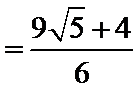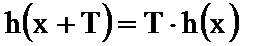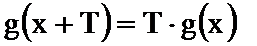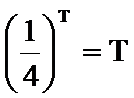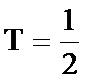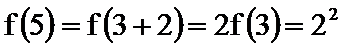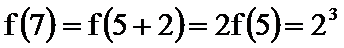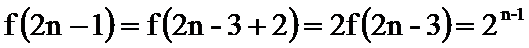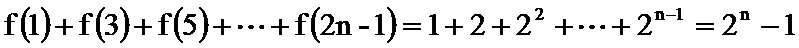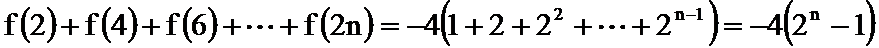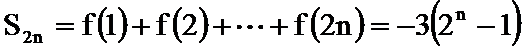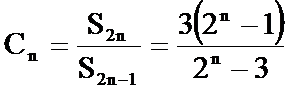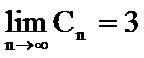- 数列与函数的综合
- 共73题
22.已知数列



(1)若


(2)设





(3)设







正确答案
(1)
(2)详见解析
(3)
解析
因为



故

(3)因为

当

当

所以
因为


①当

②当




③当






综上,

知识点
5.等比数列


正确答案
解析
等比数列中,
所以

考查方向
解题思路
利用等比数列项和项数的关系,进而求解
易错点
利用等比数列前N项和公式求解,找a1和公比q,使试题复杂。
知识点
17.设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7且a1+3,3a2,a3+4构成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=lnan,n=1,2,…,求数列{bn}的前n项和Tn.
正确答案
(Ⅰ)
(Ⅱ)
解析
(I)设{an}是公比q大于1的等比数列,∵a1+3,3a2,a3+4构成等差数列,
∴6a2=a3+4+a1+3,化为6a1q=
联立解得a1=1,q=2.∴an=2n﹣1.
(II)bn=lnan=(n﹣1)ln2,∴数列{bn}的前n项和Tn=
考查方向
解题思路
(Ⅰ)由于






(Ⅱ)把第(Ⅰ)问求得



易错点
本题在第二问构造中易出现错误
知识点
16.数列



正确答案
解析
第一种情况:当

第二种情况:当











考查方向
解题思路
由分段函数可知,若数列为等比数列,则它的公比为2,要使得数列是公比为2的等比数列,则从数列的第二项开始,都应该满足分段函数的2式,也就是
易错点
不能理解分段函数的意思
知识点
12.数列{an}的通项公式为an =
①{an}为先减后增数列;
②{an}为递减数列:
③
④
其中正确命题的序号为
正确答案
解析
先取对数得
由此可知an的单调性与
故此先研究
构造函数

所以
由此可知

又因
所以
因此函数
故{an}为递减数列,
且
故选C。
考查方向
本题主要考查了数列的单调性与有界性
解题思路
首先取对数得



易错点
对于数列单调性无从下手。
知识点
16.已知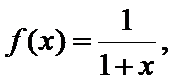
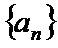
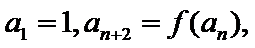
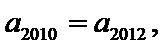
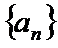
正确答案
解析
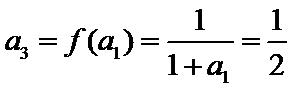
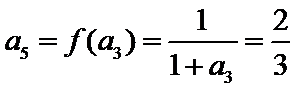
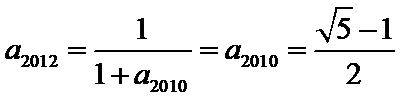
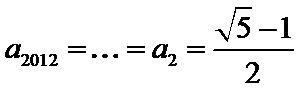
考查方向
解题思路
本题属于简单题,
(1)逐一写出数列各项
(2)找出规律后,求和
易错点
计算过程易忽略数列当中的规律
知识点
20.若实数数列



(1)若数列




(2) 求证:若数列


(3) 若数列






正确答案
(1)
(2)见解析
(3)
解析
(1)因为

所以
所以
所以

所以
(2) 假设


所以

故

假设

则

故

(3)由(Ⅱ)可知

且最多连续两项都是负数,最多连续三项都是正数.
因此存在最小的正整数


设


故有

由上可知


因为
所以当

当



记


当



此时

若


此时

当



综上可知

考查方向
本题主要考察了数列中项的问题,属于难题,是高考的热点,解决此类题的关键:是会对数列中的项进行分析。
易错点
1、本题易在对数列中的项分析不全面出现错误 。
2、对数列中项的性质研究不全面出现错误。
知识点
已知函数




(1)求证:数列
(2) 若




(3)若



正确答案
(1) 证:由题意
即
∴
∴
∵常数


∴数列


(2) 当


所以
因为

因而最小值为
(3) 由(1)知,


即

当



当




∵
∴当

∴

∴
综上所述,存在实数
解析
本题属于数列与不等式的综合应用题,题目的难度是偏难,本题的关键是:
(1)、利函数的性质求出数列的通项公式;
(2)、利用等比数列的求和公式求出前n项和的表达式,并求出最小值;
(3)、根据数学归纳法,分类讨论出k的取值范围。
考查方向
本题考查了数列的综合应用题,特别是数列与不等式之间的应用题
易错点
1、由


知识点
20.在数字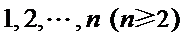
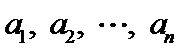
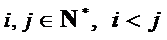
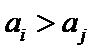
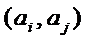
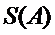
如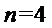
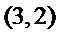
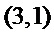
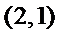
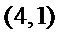
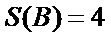
(Ⅰ)设排列 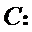
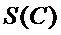
(Ⅱ)对于数字1,2,
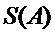
(Ⅲ)如果把排列A: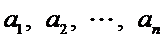

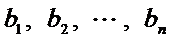
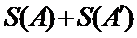
正确答案
(Ⅰ)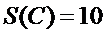
(Ⅱ)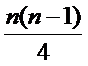
(Ⅲ)证明略。
解析
试题分析:本题属于新定义题目的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意分类讨论思想的应用
(Ⅰ)解: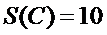
(Ⅱ)解:考察排列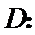
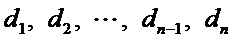
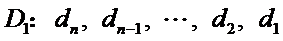
因为数对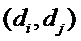
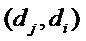
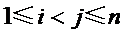
且排列D中数对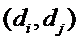
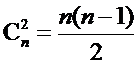
所以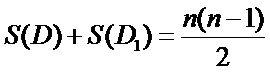
所以排列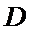
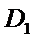
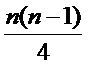
而对于数字1,2,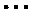
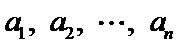
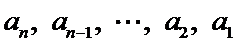
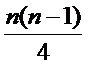
所以所有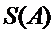
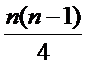
(Ⅲ)证明:①当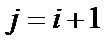
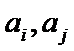
不妨设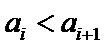
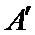
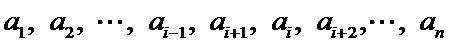
此时排列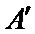
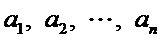

所以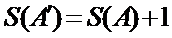
所以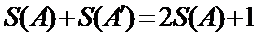
②当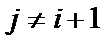
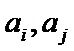
假设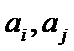
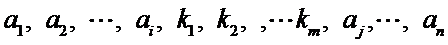
先将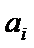
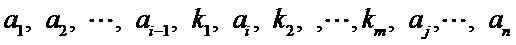
由①,知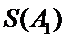
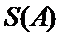
再将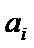
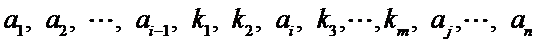
由①,知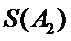
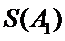
以此类推,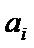
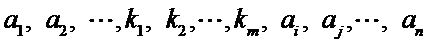
再将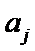
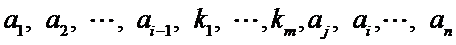
以此类推,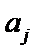
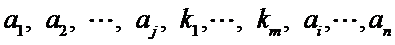
即为排列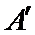
由①,可知仅有相邻两数的位置发生变化时,排列的逆序对个数的奇偶性发生变化,
而排列A经过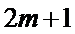
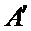
所以排列A与排列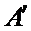
所以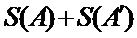
综上,得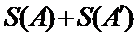
考查方向
本题主要考查了新定义的研究,对新定义问题的考查注意分以下几类:
1.与集合相关的新定义,
2.与数列相关的新定义,
3.与函数相关的新定义;与计数原理相关的新定义.
解题思路
本题考查新定义问题的考查,解题步骤如下:
1.直接写出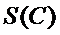
2.考查考察排列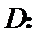
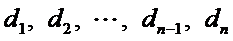
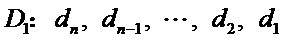
3.研究排列与逆序的个数,进而求其平均值;
4.分情况讨论研究“仅有相邻两数的位置发生变化”
易错点
1、第二问中,对“逆序”理解不透彻,导致错误;
2、第三问中,不要忽视对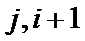
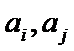
知识点
23.已知函数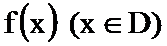
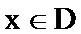
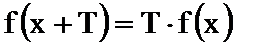
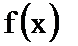
(1)判断
(2)证明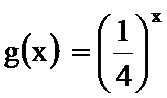
(3)若
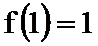
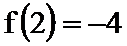
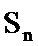
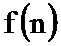
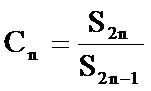
正确答案
(1)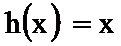
(2)证明略
(3)
解析
解:(1) 设:
则 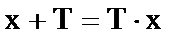
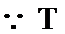
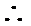
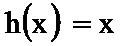
(2) 设:
则 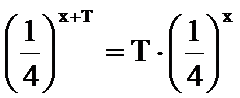
下证唯一性:
若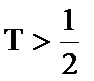
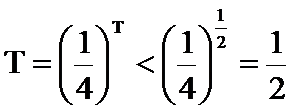
若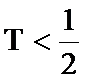
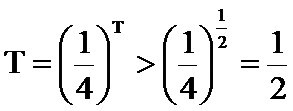
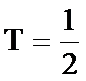
(3)
同理:
同理:
考查方向
解题思路
首先作到最后,要有耐心和信心,认真审题,发掘题目中的可利用信息。第一问直接证明有困难,可以考虑反证法;第三问因为奇数项和偶数项的变化规律不同,宜采用分组求和法。
易错点
第三问数列的奇数项和偶数项要区别对待,忽视容易产生错误。
知识点
扫码查看完整答案与解析