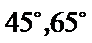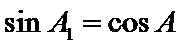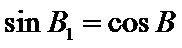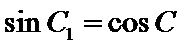三角形中的几何计算
共63题

· 三角形中的几何计算

三角形中的几何计算
共63题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

16. 在中，角所对的边分别为，且，则的最大值为 .

正确答案

解析

试题分析：由及正弦定理可知，化简得，即，所以，故，所以，此题答案为。

考查方向

本题主要考查正余弦定理及两角差的正切公式．

解题思路

由求出B-C的。

易错点

对题所给条件不知如何应用导致本题没有思路。

知识点

三角形中的几何计算

题型：单选题

单选题 · 5 分

10．在边长为2的正三角形ABC中，D为BC中点，点P是该等边三角形的三边上的动点，求的范围是( )

正确答案

解析

设AD的中点为O，那么=||2-|AD |2/2，就可以求出最值得范围

考查方向

本题主要考查了平面向量基本知识以及运动变化和函数的思想，平面向量是高考中重要的一个考点，是每年必考的，其中数量积也是高频考题。

解题思路

本题可以建立坐标系用向量建立函数关系，可以直接用向量点积的几何意义建立函数关系求解

易错点

容易选择D答案，选择两个端点检验。

知识点

三角形中的几何计算平面向量数量积的运算向量在几何中的应用

题型：填空题

填空题 · 5 分

14．已知，若存在，满足,则称是的一个“友好”三角形．

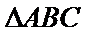
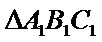
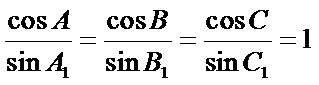
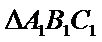
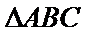
(i) 在满足下述条件的三角形中，存在“友好”三角形的是____：（请写出符合要求的条件的序号）

① ；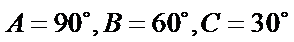

②；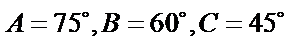

③．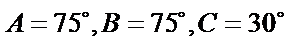

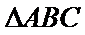
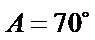
(ii) 若存在“友好”三角形，且，则另外两个角的度数分别为___．

正确答案

②；

解析

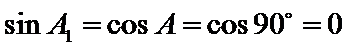
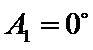
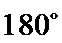
(i) ①因为，所以或，所以不存在“友好”三角形；

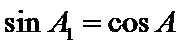
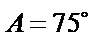
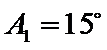
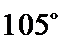
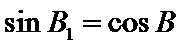
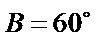
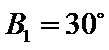
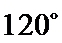
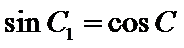
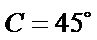
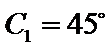
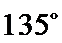
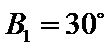
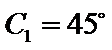
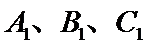
②因为，，所以或；因为，，所以或；因为，，所以或；当，，时，三点可构成三角形．存在“友好”三角形；

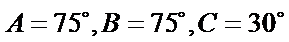
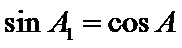
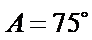
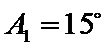
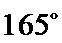
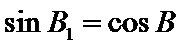
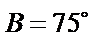
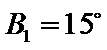
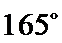
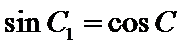
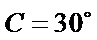
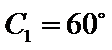
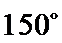
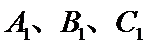
③因为，，所以或；因为，，所以或；因为，，所以或；三点无法构成三角形．不存在“友好”三角形；

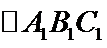
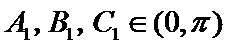
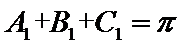
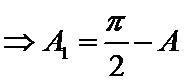
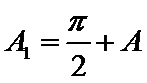
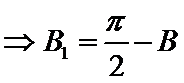
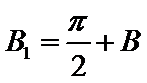
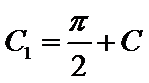
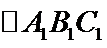
(ii) ，则，且，

或，

三角的构成，可以认为从上述方程组的解中提取组合，可以简单分成四类：

a．三个“-”；

b．三个“+”；

c．两个“-”一个“+”；

d．两个“+”一个“-”．

a．三个“-”；

（舍）．

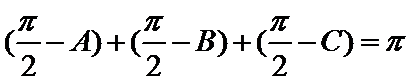
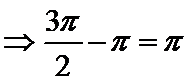
b．三个“+”；

（舍）．

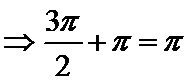
c．两个“-”一个“+”；

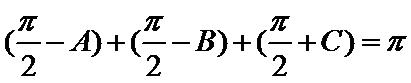
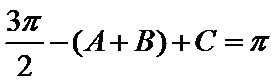
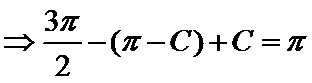
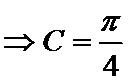
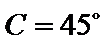
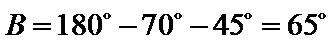
不妨设，则，即，所以．

d．两个“+”一个“-”．

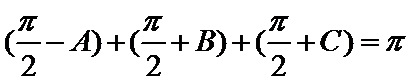
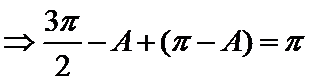
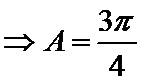
不妨设，则（舍）．

考查方向

本题考查了诱导公式，分类讨论思想，在近几年的各省高考题出现的频率较低．

解题思路

由方程、诱导公式解得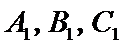，再分类讨论．

易错点

没有检查三角能不能构成三角形致误．

知识点

正弦定理三角形中的几何计算

题型：填空题

填空题 · 5 分

12.设△ABC的内角A，B，C的对边分别为a，b，c，己知(c+a-b) (b+c-a) =3ab，则角C的大小为____．

正确答案

答案：120o

解析

试题分析：本题属于解三角形问题，题目的难度较小。

考查方向

本题主要考查了解三角形。

解题思路

本题考查解三角形，解题步骤如下：

原式化为c2-a2-b2=ab；即cosC=-1/2；所以C=120o 。

易错点

本题必须注意余弦定理，忽视则会出现错误。

知识点

余弦定理三角形中的几何计算

题型：简答题

简答题 · 12 分

17.在△ABC中，角A，B，C的对边分别为a，b, c且 = .

（1）求角A的值；

（2）若∠B =，BC边上中线AM=,求△ABC的面积.

正确答案

（1）由正弦定理，

得

化简得，，

（2）可知三角形ABC为等边三角形，

在三角形AMC中，

由余弦定理，

可得

解得，AC=b=2，

所以，

解析

，，

化简得，A=30度，

可知三角形ABC是等腰三角形，

由余弦定理可得，b=2,

所以面积为

考查方向

本题主要考查正弦定理和余弦定理的性质，属于基础题

解题思路

先用正弦定理求A,然后利用余弦定理求三角形的面积

易错点

混淆两个定理的性质

知识点

正弦定理三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 解三角形的实际应用

百度题库 > 高考 > 文科数学 > 三角形中的几何计算

扫码查看完整答案与解析