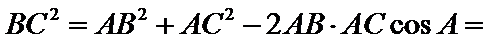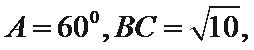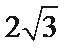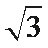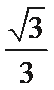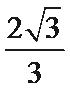三角形中的几何计算
共63题

· 三角形中的几何计算

三角形中的几何计算
共63题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

12．若锐角的面积为，且，则等于________．

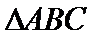
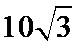
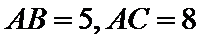
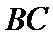
正确答案

解析

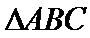
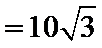
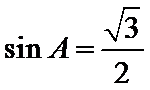
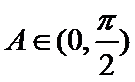
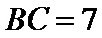
由已知得的面积为，所以，，所以．由余弦定理得，．

考查方向

1、三角形面积公式；2、余弦定理．

解题思路

利用三角形的面积公式求出A，再利用余弦定理求出BC.

易错点

计算能力弱，不会用余弦定理求三角形的面积

知识点

正弦定理余弦定理三角形中的几何计算

题型：简答题

简答题 · 20 分

本题包括A、B、C、D四小题，请选定其中两小题，并在相应的答题区域内作答，若多做，则按作答的前两小题评分，解答时应写出文字说明、证明过程或演算步骤．

材料A．[选修4-1：几何证明选讲]（回答30题）

如图，在中，，，为垂足，是中点．

材料B．[选修4-2：矩阵与变换]（回答31题）

已知矩阵，矩阵的逆矩阵，

材料C．[选修4-4：坐标系与参数方程]（回答32题）

在平面直角坐标系中，已知直线的参数方程为，椭圆的参数方程为，设直线与椭圆相交于两点，

材料D．[选修4-5：不等式选讲]（回答33题）

设，，，

回答下列问题

30.求证：．

31.求矩阵．

32.求线段的长．

33.求证：．

第(1)小题正确答案及相关解析

正确答案

由可得，

由是中点可得，

则，

由可得，

因此，

又可得．

解析

由可得，

由是中点可得，

则，

由可得，

因此，

又可得．

考查方向

相似三角形

解题思路

先由直角三角形斜边上中线性质，再由，与互余，与互余，等角关系：，从而得证

易错点

平面几何基本定理的应用

第(2)小题正确答案及相关解析

正确答案

；

解析

，因此．

考查方向

逆矩阵，矩阵乘法

解题思路

易错点

逆矩阵的转化运算

第(3)小题正确答案及相关解析

正确答案

；

解析

直线方程化为普通方程为，

椭圆方程化为普通方程为，

联立得，解得或，

因此．

考查方向

直线与椭圆参数方程

解题思路

易错点

参数方程与普通方程的互化。

第(4)小题正确答案及相关解析

正确答案

可得，

解析

由可得，

．

考查方向

含绝对值的不等式证明

解题思路

利用含绝对值的不等式进行放缩证明

易错点

绝对值三角不等式的模式与应用。

题型：单选题

单选题 · 5 分

11. 在中，是边上的一点，，的面积为，则的长为（）

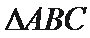
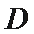
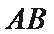
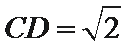
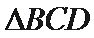
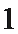
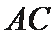
正确答案

解析

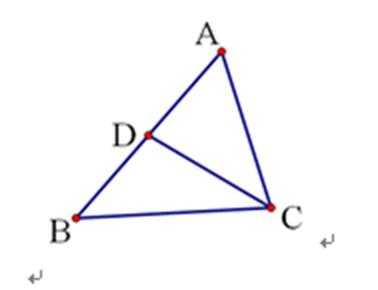
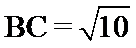
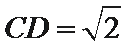
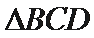
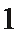
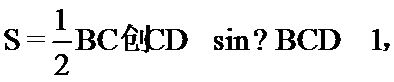
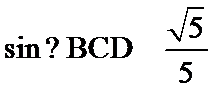
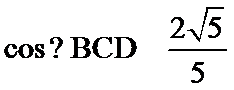
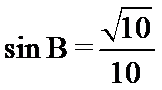
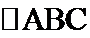
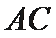
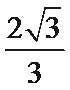
如图所示：由,，的面积为,所以有则可以得到，所以，在三角形BCD中由余弦定理可以算出BD的长度为2，在此三角形中由正弦定理可以得,在中由正弦定理即可算出=，所以选D答案。

考查方向

正余弦定理的应用。

解题思路

先画出示意图，再利用定理解决。

易错点

不会灵和使用定理来求解。

知识点

三角形中的几何计算

题型：填空题

填空题 · 5 分

11．已知菱形的边长为2，，点分别在边上，，若，则的值为___________

正确答案

解析

由得：

考查方向

本题主要考查了平面向量的应用。

解题思路

本题考查运用平面向量在几何中的应用，解题步骤如下：建立如图所示直角坐标系，

则，由得：

易错点

本题必须注意审题，忽视则会出现错误。

知识点

三角形中的几何计算平面向量数量积的运算向量在几何中的应用

题型：单选题

单选题 · 5 分

4.△ABC的内角A、B、C的对边分别为a、b、C.已知，，，则b=（）

正确答案

知识点

三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 解三角形的实际应用

百度题库 > 高考 > 文科数学 > 三角形中的几何计算

扫码查看完整答案与解析