三角形中的几何计算
共63题

· 三角形中的几何计算

三角形中的几何计算
共63题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

17．已知函数f（x）＝2＋sin2x．

（Ⅰ）求函数f（x）的对称轴所在的直线方程；

（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且f（C）＝3，c＝1，ab＝2，

且a＜b，求a，b的值．

正确答案

（1）；（2） ∴ ，

解析

试题分析：本题属于简单的三角恒等变换及正余弦定理解三角型的问题，（1）先用辅助角公式化简再进一步求解，（2）利用余弦定理最后再构造方程组来解答。

17解：（Ⅰ）

对称轴所在的直线方程为： …………(6分)

（Ⅱ）

是三角形内角

∴， ∴ 即：

∴ 即：

由得：，代入上式可得：解之得：

∴

∴ …………(12分)

考查方向

本题考查了简单的三角恒等变换及正余弦定理解三角型的问题。

解题思路

本题考查简单的三角恒等变换及正余弦定理解三角型，解题步骤如下：（1）先用辅助角公式化简再进一步求解，（2）利用余弦定理最后再构造方程组来解答。

易错点

不会使用辅助角公式合二为一。

知识点

三角函数中的恒等变换应用三角形中的几何计算

题型：简答题

简答题 · 12 分

16．在△ABC中，角A，B，C的对边分别为a，b，c，向量和向量为共线向量．

（Ⅰ）求角的大小；

（Ⅱ）若a＝6，求△ABC面积的最大值．

正确答案

（1）；（2）。

解析

试题分析：本题属于向量结合三角函数以及解三角形的知识

（1）根据向量共线的坐标表示得到一个等式，再利用正弦定理实现边角互化从而可以解出角A；

（2）先由余弦定理再结合基本不等式即可。

（Ⅰ）因为向量和向量为共线向量，

所以，由正弦定理得，

即．

由于B是三角形的内角，，则，所以.

（Ⅱ）因为，

所以，

且仅当b=c时取得等号，所以，故，

所以当b＝c时，△ABC面积的最大值为

考查方向

本题考查了向量结合三角函数以及解三角形的知识。

解题思路

本题考查向量结合三角函数以及解三角形的知识，解题步骤如下：

（1）根据向量共线的坐标表示得到一个等式，再利用正弦定理实现边角互化从而可以解出角A；

（2）先由余弦定理再结合基本不等式即可。

易错点

不能联想到基本不等式。

知识点

正弦定理余弦定理三角形中的几何计算

题型：填空题

填空题 · 5 分

14.如图6，为了测量、两点间的距离，选取同一平面上、两点，测出四边形各边的长度（单位：）：，，，，且与互补，

则的长为_____.

正确答案

解析

在三角形ABC中，由余弦定理得，

在三角形ACD中，由余弦定理得，

因为A+C=180，所以，所以，所以，所以AC=7

考查方向

解三角形的实际应用

解题思路

分别在三角形ABC和三角形ACD中使用余弦定理解出AC,列方程解出cosD,最后求出AC

易错点

计算错误,实际问题转化成数学模型的能力

知识点

三角形中的几何计算解三角形的实际应用

题型：简答题

简答题 · 14 分

如图，在四边形中，=，且，，．

16.求的面积；

17.若，求的长．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅰ）

因为，所以，

所以△ACD的面积．

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用已知条件求出∠D角的正弦函数值，然后求的面积；

易错点

主要易错于计算出错，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅱ）在△ACD中，，

所以．

在△ABC中，

把已知条件代入并化简得：因为，所以

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用已知条件求出∠D角的正弦函数值，然后求的面积；

易错点

主要易错于计算出错，

题型：填空题

填空题 · 5 分

16.在中，内角的的对边分别为，且，若是边上一点且，则．

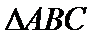
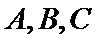
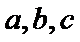
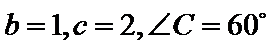
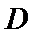
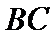
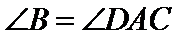
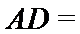
正确答案

解析

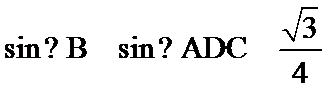
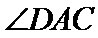
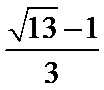
在三角形ABC中由正弦定理可以求出,再求出的正弦值，在三角形ADC中再用正弦定理即可解出AD=。

考查方向

正余弦定理解三角形。

解题思路

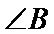
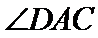
本题考查正余弦定理解三角形的能力，解题步骤如下：先用正弦定理求出的正弦值，然后求出的正弦值，再用正弦定理即可解出。

易错点

不会灵和应用定理解答。

知识点

正弦定理余弦定理三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 解三角形的实际应用

百度题库 > 高考 > 文科数学 > 三角形中的几何计算

扫码查看完整答案与解析