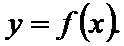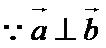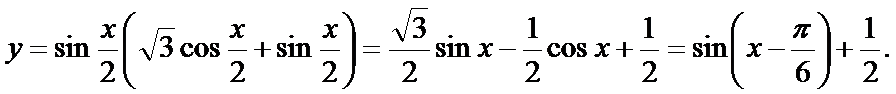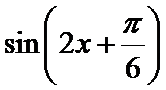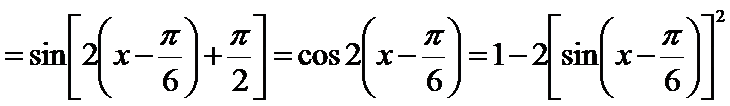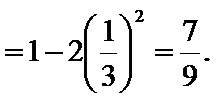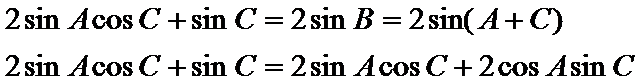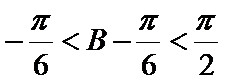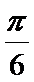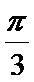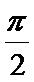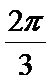- 三角形中的几何计算
- 共63题
已知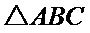
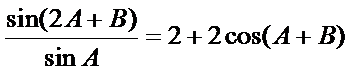
17.求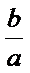
18.若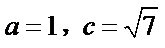
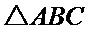
正确答案
(1)
解析
(Ⅰ)∵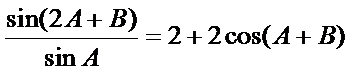
∴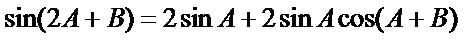
∴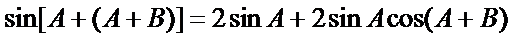
∴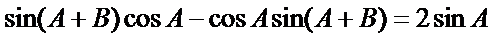
∴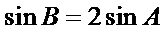
∴
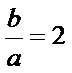
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到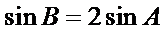
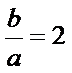
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角
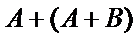
2)第二问中用余弦定理求角时容易将特殊角记错。
正确答案
(2)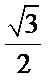
解析
(Ⅱ)∵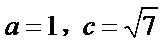
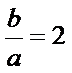
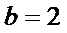
∴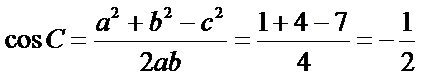
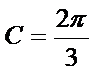
∴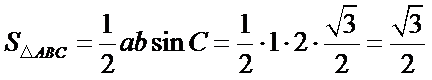
即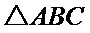
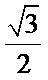
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到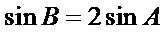
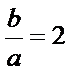
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角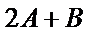
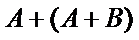
2)第二问中用余弦定理求角时容易将特殊角记错。
13.设△




正确答案

解析
由








考查方向
解题思路
1.先根据正弦定理将角间的关系转化为边
易错点
不会将题中的条件
知识点
已知向量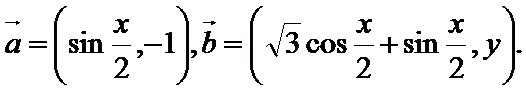
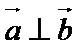
17.若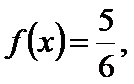
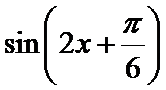
18.在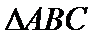
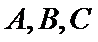
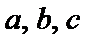
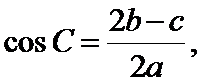
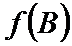
正确答案
解析
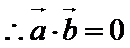
得
即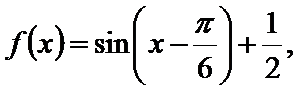
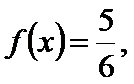
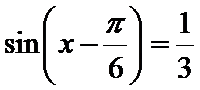
考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-
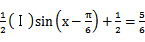
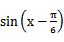

易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由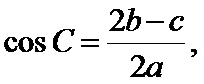
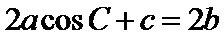
∴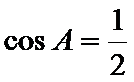

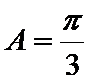
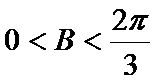
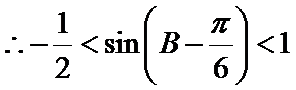
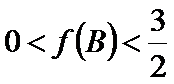
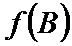
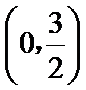
考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
5.设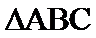
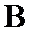
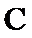
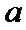
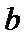
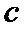
若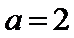
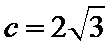
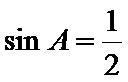

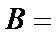
正确答案
解析
由题意可知,由正弦定理可得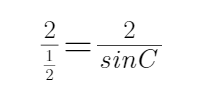
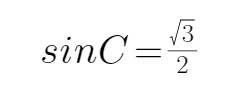
而A=30度,当C=60度时,B=90度,不符合b<c
当C=120度,B=30度,符合,所以选A
考查方向
正弦定理的性质和应用
解题思路
利用正弦定理求出角C的大小,然后求角B的大小
易错点
正弦定理公式记忆混淆
知识点
扫码查看完整答案与解析