- 生活中的圆周运动
- 共107题
16.如图所示,ABC是半径R=m的光滑圆弧轨道,A点和圆弧圆心O的连线与竖直方向的夹角θ=37°,C端在圆弧轨道圆心O的正下方,现在某一位置水平抛出一个质量m=2kg的小滑块(可视为质点),并恰好从轨道的上端A点以速度vA=4m/s沿圆弧切线进入轨道,从轨道末端C点滑上了与它等高的足够长的木板,小物块与木板间的动摩擦因数μ=0.5,水平面光滑且右边有竖直的挡板P,挡板P与C间的距离足够远,设长木板与挡板P碰撞无机械能损失,长木板的质量M=1kg.(g取10m/s2),
试求:
(1)小物块的抛出点到O的竖直距离.
(2)小物块经过圆弧轨道上A点的正下方B点时对轨道的压力的大小.
(3)从小物块滑上长木板到长木板第三次与挡板P碰撞前小物块变速运动的时间和小物块距长木板左端的距离.
正确答案
解:(1)由平抛运动规律可知,小球达到A点时的竖直分速度vy=vsin37°=4×0.6=2.4m/s;
则由vy2=2gH可得:
抛出点到A点的距离:H=
故抛出点到O点距离:
H′=0.288+
(2)由AC过程由机械能守恒定律可得:
mg(R+Rcos37°)=mvC2﹣mvA2
由牛顿第二定律可知:
FN﹣mg=m
解得:
vc=5m/s;
FN=220N;
(3)由牛顿第二定律可知,物体的加速度a1=μg=0.5×10=5m/s2;
木板的加速度a2=

物体滑到木板上后,物体做减速运动,木板做加速运动,设经时间t达到相对速度,则有:
vC﹣a1t=a2t
解得:t1=s;
因距离足够长,故碰前达共同速度,共同速度v2=a2t=10×=
此时二者之间的相对位移△x1=


碰后,二者速度反向,木板以
设经时间t2木板静止,则有:
t2=

木板向左运动的位移x=

此时物体的速度v3=v2﹣a1t2=
此物块向右的位移
x木2=
物体向右增加的位移△x2=

木板再向右加速,达到相同速度用时t3=s;此时没有相碰;
共同速度v4=a2t3=10×=
物体向右运动的位移△x3=


故第3次碰撞前用时t=t1+t2+t3=++=s;
物体相对木板的位移△x=△x1+△x2+△x3=



解析
解析已在路上飞奔,马上就到!
知识点
12.长为L的轻绳的一端固定在O点,另一端栓一个质量为m的小球。先令小球以O为圆心,L为半径在竖直平面内做圆周运动,小球能通过最高点,如图所示。g为重力加速度。则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图甲所示,轻杆一端与质量为1 kg、可视为质点的小球相连,另一端可绕光滑固定轴在竖直平面内自由转动。现使小球在竖赢平面内做圆周运动,经最高点开始计时,取水平向右为正方向,小球的水平分速度w随时间f的变化关系如图乙所示,A、B、C三点分别是图线与纵轴、横轴的交点、图线上第一周期内的最低点,该三点的纵坐标分别是1、0、-5。g取10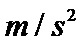
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=10m,半圆形轨道半径R=2.5m。质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道运动到最高点C,从C点水平飞出。重力加速度g取10m/s2。若小滑块从C点水平飞出后又恰好落在A点。
试分析求解:
(1)滑块通过C点时的速度大小;
(2)滑块刚进入半圆形轨道时,在B点对轨道的压力大小;
(3)水平力F 的大小。
正确答案
解:(1)设滑块从C点飞出时的速度为vC,从C点运动到A点时间为t,滑块从C点飞出后,做平抛运动
竖直方向:2R=
水平方向:x=vCt
解得:vC=10m/s
(2)设滑块通过B点时的速度为vB,根据机械能守恒定律




设滑块在B点受轨道的支持力为FN,根据牛顿第二定律
FN-mg=m
联立解得:FN= 9N
依据牛顿第三定律,滑块在B点对轨道的压力F¢N= FN=9N
(3)若滑块恰好能够经过C点,设此时滑块的速度为v¢C,依据牛顿第二定律有
mg=m
解得v¢C=

滑块由A点运动到C点的过程中,由动能定理
Fx- mg×2R≥
Fx≥mg×2R+
解得水平恒力F应满足的条件 F≥0.625N
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,可以看成质点的小物体放在高度为h=1.25 m.长度为s=1.25 m的粗糙水平固定桌面的左端A点,以初速度vA=5 m/s向右滑行,离开桌子边缘B做平抛运动,落入光滑竖直圆轨道的缺口C中,速度vC与圆轨道相切,然后在圆轨道中运动,恰好能够经过圆轨道的最高点D.已知物体在D点的速度vD=0.5 vC ,半径OC与竖直方向夹角为60°,小物体质量m=1 kg(g取10 m/s2).
(1)小物体离开桌子边缘B后经过多长时间落地?
(2)小物体与桌面之间的动摩擦因数为多大?
(3)圆轨道的半径R等于多少?
(4)小物体运动到C的对称点C′时对轨道的压力是多大?
正确答案
(1)0.5s
(2)0.67
(3)0.83
(4)45N
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,PA是半径为R的四分之一光滑圆弧轨道,AB为一段粗糙的水平轨道,二者相切于A点,AB离水平地面高h=0.45m,BC是倾角为θ=37°的斜面,三段轨道处于同一竖直面内。现将质量m=1.0kg的小滑块从P点由静止释放。已知圆弧轨道的半径R=0.9m,滑块与AB轨道之间的动摩擦因数μ=0.2,(取g=10m/s2,sin37°=0.6,cos37°=0.8.)
(1)求滑块刚到达A点时对A点的压力。
(2)若要使滑块不能落到BC斜面上,AB段的长度应满足什么条件。
正确答案
解:(1)设滑块到A点的速度为vA,刚到达A点时受到的支持力为F,
根据机械能守恒有:mvA2/2=mgR,
根据牛顿第二定律有:F−mg=mv2/R
代入数据解得F=30N.
由牛顿第三定律得,滑块对A点的压力为30N,方向垂直AB向下
(2)设AB的长度为L1,滑块刚好能运动到B点,
由动能定理得,mgR=μmgL1,
代入数据解得L1=4.5m.
设AB的长度为L2时,滑块离开B点后做平抛运动刚好落到C点,
设离开B点的速度为vB,
根据平抛运动的知识,
有:h=gt2/2,hcotθ=vBt,
代入数据解得vB=2m/s.
根据动能定理得,mgR-μmgL2=mvB2/2
解得L2=3.5m.
故AB的长度L应该满足L>4.5m或L<3.5m.
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内,轨道的B端切线水平,且距水平地面高度为h=1.25m,现将一质量m=0.2kg的小滑块从A点由静止释放,滑块沿圆弧轨道运动至B点以v=5m/s的速度水平飞出(g取10m/s2).求:
(1)小滑块沿圆弧轨道运动过程中所受摩擦力做的功;
(2)小滑块经过B点时对圆轨道的压力大小;
(3)小滑块着地时的速度大小。
正确答案
(1)由动能定理有

(2)设轨道对滑块的支持力为N,由牛顿第二定律有
得N=4.5N
由牛顿第三定律知滑块对B的压力为4.5N,方向竖直向下。
(3)滑块过B点后作平抛运动,设着地时竖直速度为
所以
解析
解析已在路上飞奔,马上就到!
知识点
21.如图所示,一倾角为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.如图为某工厂生产流水线上水平传输装置的俯视图,它由传送带和转盘组成.物品从A处无初速度放到传送带上,运动到B处后进入匀速转动的转盘,设物品进入转盘时速度大小不发生变化,此后随转盘一起运动(无相对滑动)到C处被取走装箱.已知A、B两处的距离L=10 m,传送带的传输速度V=2 m/s,物品在转盘上与轴O的距离R=4 m,物品与传送带间的动摩擦因数
(1)物品从A处运动到B处的时间t.
(2)质量为m=2 kg的物品随转盘一起运动的静摩擦力为多大.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图所示,倾角为37
(取
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析