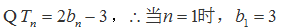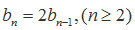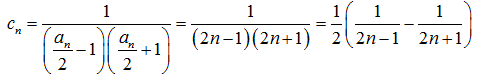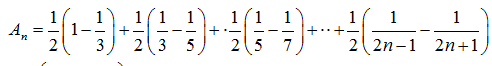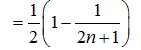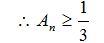- 数列与不等式的综合
- 共81题
10.已知数列

正确答案
解析
由于t<a1<t+1,得a2=a1-t,易得0<a1-t<1,即0<a2<1
又t>2,那么a3=t+2-a2=2t+2-a1
又t+1<2t+2-a1<t+2,即t+1<a3<t+2;a4=a3-t=t+2-a1,
又1<t+2-a1<2,即1<a4<2,得a4<t
从而a5=t+2-a4=a1
结合an+k=an(k∈N*),可得实数k的最小值为4.
知识点
10.已知数列

正确答案
解析
由于t<a1<t+1,得a2=a1-t,易得0<a1-t<1,即0<a2<1
又t>2,那么a3=t+2-a2=2t+2-a1,
又t+1<2t+2-a1<t+2,即t+1<a3<t+2;a4=a3-t=t+2-a1,
又1<t+2-a1<2,即1<a4<2,得a4<t,
从而a5=t+2-a4=a1,结合an+k=an(k∈N*)
可得实数k的最小值为4.
知识点
23. 已知数列


(1)若


(2)设




(3)设




正确答案
(1)
(2)见解析
(3)
解析
(1)由

故
所以
(2)由
得



因为
所以

故

(3)因为

当
=
当


因为



特别地

此时对任意

当


由指数函数的单调性知,


最小值为
由题意,


由

解得
综上所述,

知识点
18. 已知数列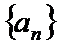
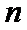
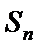
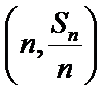
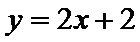
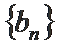
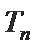
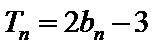
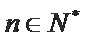
(Ⅰ)求数列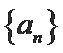
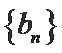
(Ⅱ)设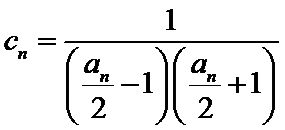
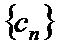
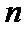
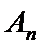
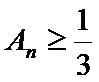
正确答案
(1)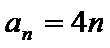
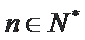
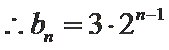
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 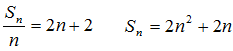
当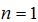
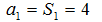
当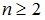
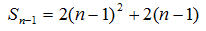
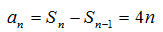
综上,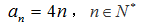
又
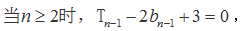
数列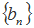
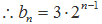
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
16.已知数列



正确答案
6
解析


同理


考查方向
解题思路
先写出递推关系,再带入进行检验
易错点
弄错递推公式。
知识点
扫码查看完整答案与解析