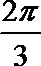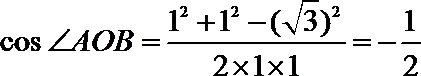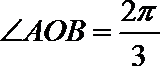- 球面距离及相关计算
- 共11题
16.已知三棱柱



正确答案
解析
因为侧棱垂直于底面,棱柱的体积为



又因为




考查方向
解题思路
利用垂直和棱柱体积求出AA1,再求出三角形ABC外接圆的半径,即可得到球的半径,从而求出球的表面积
易错点
计算能力;立体感
知识点
如图4,已知四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD
中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
22.若二面角P—CD—B为45°,求证:平面

23.在(Ⅰ)的条件下,求点A到平面PBC的距离.
正确答案
(1)略;
解析
Ⅰ)
∵AB//CD,AB⊥AD,∴


∴

取PD的中点E,PC的中点F,连结AE,BF,EF,
则


∴





∴四边形ABFE为平行四边形,∴


∵


考查方向
解题思路
1.先找出


易错点
不会从图形中找到二面角P—CD—B的平面角;
不知道该证明哪条直线垂直于哪个平面;
正确答案
(2)
解析
(Ⅱ)设点A到平面PBC的距离为



考查方向
解题思路
1.先找出


2.利用等体积法直接求解答案即可。
易错点
利用等体积法运算时求解算数出错。
6. 已知地球半径约为6371千米.上海的位置约为东经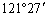
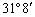
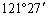
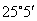
正确答案
673
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,半径为










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,正方体

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若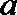
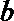
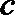
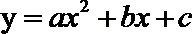
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.下列四个命题中错误的个数是( )
①经过球面上任意两点,可以作且只可以作一个球的大圆;
②球面积是它大圆面积的四倍;
③球面上两点的球面距离,是这两点所在截面圆上以这两点为端点的劣弧的长;
④若三球的半径之比是1∶2∶3,那么半径最大的球体积是其余两球体积和的3倍.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知四面体

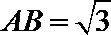


正确答案
解析
由四面体

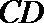

球的半径
∴
∴
∴
∴



考查方向
本题考查球面距离及其相关计算,考查空间想象能力、计算、逻辑思维能力,是中档题.
解题思路
先求球半径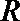
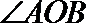

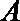


易错点

知识点
如图,半径为
















正确答案
解析
以O为原点,分别以OB、OC、OA所在直线为x、y、z轴,

知识点
18.行驶中的汽车,在刹车时由于惯性的作用,要继续往前滑行一段距离才能停下,这段距离称为刹车距离。在某种路面上,某种型号汽车的刹车距离





(1)求
(2)要使刹车距离不超过12.6米,则行驶的最大速度应为多少?
正确答案
(1)
(2)
∴行驶的最大速度应为
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析