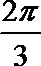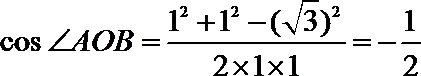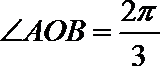球面距离及相关计算
共11题

· 球面距离及相关计算

球面距离及相关计算
共11题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

16．已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，则此球的表面积等于__________.

正确答案

解析

因为侧棱垂直于底面，棱柱的体积为，，，所以

，所以

又因为，所以,设三角形ABC外接圆的半径为R.则，所以，所以外接球的半径为。所以球的表面积为

考查方向

球的体积和表面积

解题思路

利用垂直和棱柱体积求出AA1，再求出三角形ABC外接圆的半径，即可得到球的半径，从而求出球的表面积

易错点

计算能力；立体感

知识点

球面距离及相关计算

题型：简答题

简答题 · 12 分

如图4，已知四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD

中，∠A=90°，AB∥CD，AB=1，AD=CD=2.

22.若二面角P—CD—B为45°，求证：平面平面；

23.在（Ⅰ）的条件下，求点A到平面PBC的距离.

第(1)小题正确答案及相关解析

正确答案

（1）略；

解析

Ⅰ）平面ABCD，

∵AB//CD，AB⊥AD，∴

平面，CD⊥PD，

∴二为面角P—CD—B的平面角，

，

取PD的中点E，PC的中点F，连结AE，BF，EF，

则，∵平面，

∴,平面，-∵且，，

∴四边形ABFE为平行四边形，∴，平面，

∵面，∴平面平面

考查方向

本题主要考查空间线面的位置关系、二面角和点到平面的距离等知识，意在考查考生的空间想象能力和运算求解能力。

解题思路

1.先找出二为面角P—CD—B的平面角，后证明平面，即可证明面面垂直；2.利用等体积法直接求解答案即可。

易错点

不会从图形中找到二面角P—CD—B的平面角；

不知道该证明哪条直线垂直于哪个平面；

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（Ⅱ）设点A到平面PBC的距离为，由得分

即点A到平面PBC的距离为

考查方向

本题主要考查空间线面的位置关系、二面角和点到平面的距离等知识，意在考查考生的空间想象能力和运算求解能力。

解题思路

1.先找出二为面角P—CD—B的平面角，后证明平面，即可证明面面垂直；

2.利用等体积法直接求解答案即可。

易错点

利用等体积法运算时求解算数出错。

题型：单选题

单选题 · 5 分

4．若、、成等比数列，则函数的图象与x轴的交点个数为（）

D不能确定

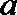
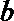
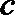
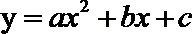
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球面距离及相关计算

题型：单选题

单选题 · 5 分

11．下列四个命题中错误的个数是（）

①经过球面上任意两点，可以作且只可以作一个球的大圆；

②球面积是它大圆面积的四倍；

③球面上两点的球面距离，是这两点所在截面圆上以这两点为端点的劣弧的长；

④若三球的半径之比是1∶2∶3，那么半径最大的球体积是其余两球体积和的3倍．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用球面距离及相关计算球的体积和表面积

题型：填空题

填空题 · 4 分

10．已知四面体的外接球球心在棱上，，，则、两点在四面体的外接球上的球面距离是___________．

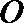
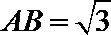
正确答案

解析

由四面体的外接球球心在棱上，，得

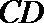
球的半径

∴

∴、两点在四面体的外接球上的球面距离为．

考查方向

本题考查球面距离及其相关计算，考查空间想象能力、计算、逻辑思维能力，是中档题．

解题思路

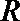
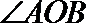
先求球半径，再求的大小，然后利用公式求得、两点在四面体的外接球上的球面距离．

易错点

在球上的位置关系不明确，从而影响球面距离的求解．

知识点

球面距离及相关计算与球体有关的内切、外接问题

继续学习学习下一知识点

下一知识点 : 组合几何体的面积、体积问题

百度题库 > 高考 > 理科数学 > 球面距离及相关计算

扫码查看完整答案与解析