- 相似三角形的判定
- 共32题
1
题型:简答题
|
圆的两弦AB、CD交于点F,从F点引BC的平行线和直线AD交于P,再从P引这个圆的切线,切点是Q。
求证:PF=PQ。
正确答案
见解析。
解析
因为A,B,C,D四点共圆,所以ADF=ABC,
因为PF∥BC,所以AFP=ABC,所以AFP=FQP,
又因为APF=FPA,
所以△APF∽△FPQ,
所以

因为PQ与圆相切,所以
所以
知识点
相似三角形的判定
1
题型:简答题
|
如图,





(1)证明:
(2)证明:
正确答案
见解析
解析
(1)由切割线定理知

(2)由


又四边形GEDF四点共圆,所以
故
知识点
相似三角形的判定
1
题型:简答题
|
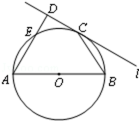
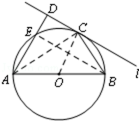
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,求线段AE的长。
正确答案
见解析
解析
连接OC,BE,AC,则BE⊥AE。
∵BC=4,∴OB=OC=BC=4,即△OBC为正三角形,
∴∠CBO=∠COB=60°。
又直线l切⊙O与C,∴OC⊥l,
∵AD⊥l,∴AD∥OC。
∴∠EAB=∠COB=60°。
在Rt△BAE中,∴∠EBA=30°,
∴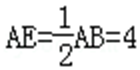
知识点
相似三角形的判定
1
题型:简答题
|
如图,






求证:(1)
(2)
正确答案
见解析
解析
证明:(1)

(2)








知识点
相似三角形的判定
1
题型:简答题
|
如图,














(1)求证:
(2)若

正确答案
见解析。
解析
(1)证明:连结




在

又∵
∴
(2)∵
∵


又因为
∴
知识点
相似三角形的判定
下一知识点 : 相似三角形的性质
扫码查看完整答案与解析