裂项相消法求和
共41题

· 裂项相消法求和

裂项相消法求和
共41题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

为数列{}的前项和.已知＞0，=.

17.求{}的通项公式；

18.设 ,求数列{}的前项和.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）

解析

（Ⅰ）当时，，因为，所以=3，

当时，==，即，因为，所以=2，

所以数列{}是首项为3，公差为2的等差数列，

所以=；

考查方向

本题考查了数列前n项和与第n项的关系；等差数列定义与通项公式；拆项消去法。

解题思路

（Ⅰ）先用数列第项与前项和的关系求出数列{}的递推公式，可以判断数列{}是等差数列，利用等差数列的通项公式即可写出数列{}的通项公式；

易错点

本题在用公式法计算通项公式时n=1易丢.

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）【考查方向】本题考查了数列前n项和与第n项的关系；等差数列定义与通项公式；拆项消去法。

解析

（Ⅱ）由（Ⅰ）知，=，

所以数列{}前n项和为= =.

解题思路

（Ⅱ）根据（Ⅰ）数列{}的通项公式，再用拆项消去法求其前项和.

易错点

本题在裂项中错出现错误。

题型：简答题

简答题 · 12 分

已知各项均不相等的等差数列的前四项和为16，且成等比数列.数列满足.

22.求数列的通项公式的前n项和；

23.是否存在正整数，使得成等比数列？若存在，求出

第(1)小题正确答案及相关解析

正确答案

见解析

解析

考查方向

本题考察了等差、等比数列的基本运算，考察了利用裂项相消法求和，考察了不等式的整数解。

解题思路

借助等差数列前4项和，与成等比数列写出方程组解出答案。

解析式裂项，求前n项和

易错点

本题易错于裂项等号不成立，第二问不理解题意

第(2)小题正确答案及相关解析

正确答案

见解析

解析

考查方向

本题考察了等差、等比数列的基本运算，考察了利用裂项相消法求和，考察了不等式的整数解。

解题思路

根据等比数列性质写出关系式

解不等式确定取值

易错点

本题易错于裂项等号不成立，第二问不理解题意

题型：单选题

单选题 · 5 分

8．已知数列{an}的各项均为正数，前n项和为Sn，且，n∈N*，则数列的前100项和为 (　　)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an裂项相消法求和

题型：简答题

简答题 · 12 分

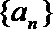
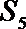
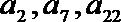
18．已知等差数列的公差不为零，其前n项和为，若=70，且成等比数列

（Ⅰ）求数列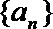的通项公式；

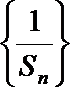
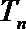
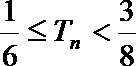
（Ⅱ）设数列的前n项和为，求证：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项裂项相消法求和数列与不等式的综合等差数列与等比数列的综合

题型：填空题

填空题 · 5 分

8.在数列{an}中，a1＝6，且对任意大于1的正整数n，点（，）在直线x－y＝上，则数列{}的前n项和Sn＝_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和

题型：填空题

填空题 · 5 分

10．若数列中，，其前n项的和是，则在平面直角坐标系中，直线在y轴上的截距为__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

裂项相消法求和直线的截距式方程

题型：简答题

简答题 · 12 分

19．已知函数，数列满足条件：．

（1）求证：数列为等比数列；

（2）令是数列的前项和，求使成立的最小的值．

正确答案

（1）证明：由题意得，∴

又 ∵

∴

故数列{bn + 1}是以1为首项，2为公比的等比数列

（2）由（1）可知，，∴

故

∴

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的判断与证明裂项相消法求和数列与函数的综合数列与不等式的综合

题型：简答题

简答题 · 16 分

19. 设数列的前项和，，，且当时，．

（1）求证:数列是等比数列，并求数列的通项公式；

（2）令，记数列的前项和为．设是整数，问是否存在正整数，使等式成立？若存在，求出和相应的值；若不存在，说明理由．

正确答案

见解析

解析

解：（1）当时, ,,

代入并化简得,

而恒为正值,∴

∴数列是等比数列.

∴.当时,,

又，∴

（2）当时，,此时，又

∴.

故，

当时，

，

若，

则等式为，不是整数，不符合题意；

若，则等式为，

∵是整数, ∴必是的因数, ∵时

∴当且仅当时，是整数，从而是整数符合题意.

综上可知，当时，存在正整数，使等式成立，

当时，不存在正整数使等式成立.

考查方向

本题考查了等比数列的证明及数列的通项公式求法

解题思路

利用，得数列是等比数列.

易错点

忽略n的范围的讨论。

知识点

由an与Sn的关系求通项an等比数列的判断与证明裂项相消法求和数列与函数的综合

题型：简答题

简答题 · 12 分

17. 在等差数列中，，数列的前n项和.

（Ⅰ）求数列，的通项公式;

（Ⅱ）求数列的前n项和．

正确答案

见解析

解析

（Ⅰ）设等差数列的首项为，公差为d，则

数列的前n项和

当n=1时，，

当n2时，，对=4不成立，

所以，数列的通项公式为

（Ⅱ）n=1时，，

n2时，，

所以

n=1仍然适合上式，

综上，

考查方向

等比数列，等比数列的前n项和

解题思路

利用构造的等比数列求前n项和公式的求解

易错点

构造等比数列

知识点

由递推关系式求数列的通项公式等差数列的基本运算裂项相消法求和

题型：单选题

单选题 · 5 分

5．定义为个正数的“均倒数”，若已知数列的前项的“均倒数”为，又，则（）

正确答案

解析

由“均倒数”为得Sn=5n2，则an=10n-5,=2n-1,

则。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查数列的综合运算

解题思路

1、求出an；

2、求出bn，利用裂项相消法求和，即可得到结果。

易错点

本题易在求an时发生错误。

知识点

裂项相消法求和

继续学习学习下一知识点

下一知识点 : 倒序相加法求和

百度题库 > 高考 > 理科数学 > 裂项相消法求和

扫码查看完整答案与解析