- 平面向量数量积的运算
- 共232题
已知向量a=(1,0),b=(1,1),则
(1)与2a+b同向的单位向量的坐标表示为______;
(2)向量b-3a与向量a夹角的余弦值为______。
正确答案

解析
(1)由题意可得,2a+b=(3,1),故|2a+b|=



知识点
设




正确答案
解析
依题意,对任意实数




知识点
若向量





正确答案
解析
设





∴


∴
∴

∴
知识点
设向量









正确答案
解析
∵|













两式相减得4



知识点
已知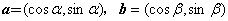
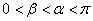
(1)若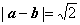
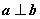
(2)设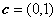
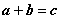
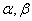
正确答案
见解析
解析
(1)a-b=(cosα-cosβ,sinα-sinβ),
|a-b|2=(cosα-cosβ)2+(sinα-sinβ)2=2-2(cosα·cosβ+sinα·sinβ)=2,
所以,cosα·cosβ+sinα·sinβ=0,
所以,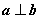
(2)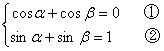
所以,α-β=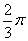
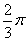
带入②得:sin(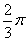
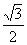
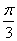
所以,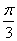
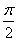
所以,α=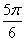
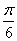
知识点
定义平面向量之间的一种运算“



正确答案
解析
若





知识点
已知向量



正确答案
解析
知识点
在平面直角坐标系




正确答案
5
解析
知识点
若非零向量


正确答案
解析
等式平方得:
则
得
知识点
已知集合




正确答案
解析



知识点
扫码查看完整答案与解析


























