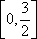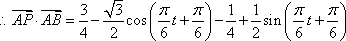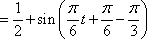- 平面向量数量积的运算
- 共232题
设e1,e2为单位向量,非零向量b=xe1+ye2,x,y∈R.若e1,e2的夹角为

正确答案
2
解析
因为b≠0,所以b=xe1+ye2,x≠0,y≠0.
又|b|2=(xe1+ye2)2=x2+y2+








知识点
已知向量

(1) 求f (x)的最小正周期.
(2)求f (x) 在
正确答案
见解析
解析
(1) 

最小正周期
所以

(2)

所以,f (x) 在

知识点
已知






③ 

⑤ 点

则正确的命题是 。(写出所有正确命题的编号)
正确答案
①③⑤
解析
略
知识点
已知








正确答案
解析
略
知识点
设函数



(1)求
(2)在






正确答案
见解析。
解析
(1)


令
解得
故
注:若没写
(2)由
而


又
知识点
已知四边形



为 .
正确答案
9
解析
略
知识点
设向量









正确答案
解析
略
知识点
已知正方形ABCD的边长为2,E为CD的中点,则
正确答案
2
解析
以

而

∴
知识点
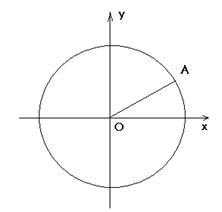
如图,设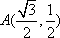
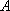
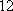
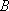


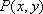
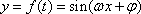
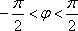
(1)求点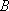
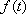
(2)若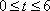
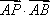
正确答案
(1)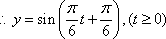
解析
(1)当

所以
所以,点B的坐标是(0,1)
又
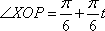
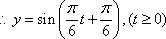
(2)由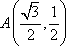
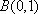
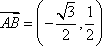
又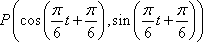
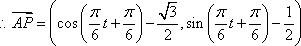
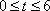
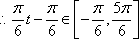
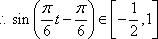
所以,

知识点
已知向量





(1)求实数
(2)若不等式


正确答案
(1)
解析
(1)由题得
又



(2)由(1)的他,
令



即





知识点
扫码查看完整答案与解析