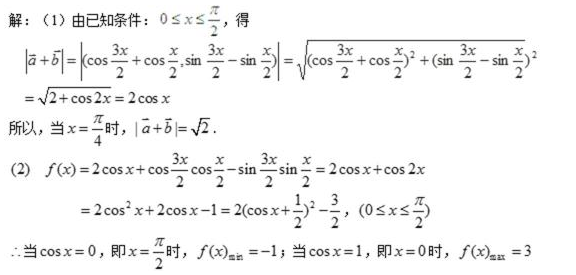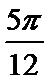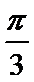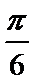- 平面向量数量积的运算
- 共232题
15. 已知







①
② 
③ 
④
⑤ 点

则正确的命题是 _____________.(写出所有正确命题的编号)。
正确答案
①③⑤
解析
解析已在路上飞奔,马上就到!
知识点
2.设向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知向量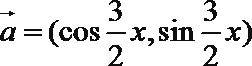
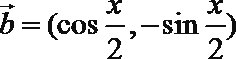
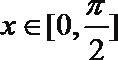
(1)当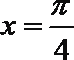
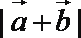
(2)设函数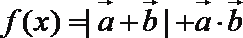
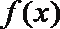
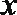
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线



(1)求抛物线

(2)过点







(3)直线













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,已知P是边长为2的正三角形的边BC上的动点,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若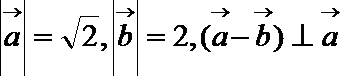
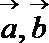
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在边长为1的正三角形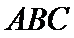
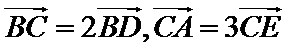
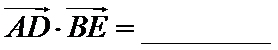
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设函数


(1)求
(2)在




正确答案
(1)因为
所以最小正周期是
(2)由

又由余弦定理得,

解①②得


解析
解析已在路上飞奔,马上就到!
知识点
18.已知圆
(1)若


(2)是否存在






正确答案
(1)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),
半径为 r = 3,
若 l与C相切,
则得
∴(3m-4)2=9(1+m2),
∴m =
(2)假设存在m满足题意。
由
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,
得m>
设A(x1,y1),B(x2,y2),
则y1+y2=


=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·
=25-
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2

∴存在m=9±2
解析
解析已在路上飞奔,马上就到!
知识点
16.在
(1)求
(2)设D为AC中点,求
正确答案
解:由题意得

(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析