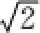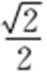- 平面向量数量积的运算
- 共232题
6.已知向量a，b，c满足
A
B
C
D
正确答案
解析
由
不妨设a=(2，0)，b=(1，
由(a-c)·(b-2c)=0可得(2-x)(1-2x)+(-y)(
整理得2x2-5x+2y2-
则
知识点
2.已知椭圆C: 
A
B
C
D
正确答案
解析
设
由条件知|AF2|为椭圆通径的一半，即|AF2|=
则
于是
易知此时点P在椭圆短轴的上顶点
所以
知识点
5.已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是（ ）
A1
B2
C
D
正确答案
解析
因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c).
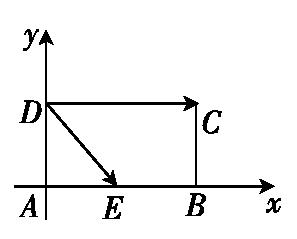
如图所示，设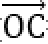
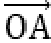
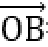
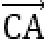
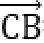
又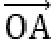
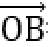
当且仅当OC为圆的直径时，|c|最大，且最大值为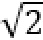
知识点
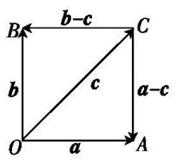
8.若a，b，c均为单位向量，且a·b=0，(a－c)·(b－c)≤0，则|a+b－c|的最大值为（ ）
A
B1
C
D2
正确答案
解析
设a=(1，0)，b=(0，1)，c=(x，y)，则x2+y2=1，
a－c=(1－x，－y)，b－c=(－x，1－y)，
则(a－c)·(b－c)=(1－x)(－x)+(－y)(1－y)=x2+y2－x－y=1－x－y≤0，即x+y≥1，
又a+b－c=(1－x，1－y)，
∴|a+b－c|=
∵c=(x，y)对应的点在
∴|a+b－c|的最大值为1.
知识点
1.已知ω>0,|φ|< 
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.已知矩形ABCD的边长AB=2，BC=1，点E是AB边上的动点，则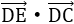
正确答案
[0，4]
解析
如图所示，以AB，AD所在的直线分别为x轴，y轴建立平面直角坐标系xAy
由于AB=2，BC=1，故B(2，0)，C(2，1)，D(0，1).
因为E在AB边上，所以可设E(t，0)(0≤t≤2).
则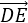
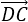
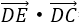
又0≤t≤2，则0≤2t≤4
所以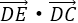
知识点
22．在△ABC中，AB＝3，AC边上的中线BD＝
（1）求AC的长；
（2）求sin（2A－B）的值
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．已知向量
（1）求角
（2）若
正确答案
（1）
（2）由
及
解析
解析已在路上飞奔，马上就到！
知识点
21．已知向量a、b、c是同一平面内的三个向量，其中a＝（1，2）．
（1）若|c|＝2
（2）若|b|＝
正确答案
（1）令c＝（x，y），则由|c|＝2
又由a∥c知，2x－y＝0②
联立①②可解得：
故c＝（2，4）或c＝（－2，－4）．
（2）由a＋2b与2a－b垂直知（a＋2b）·（2a－b）＝0，
即2a2＋3a·b－2b2＝0，∴a·b＝
即|a||b|cosθ＝
而由a＝（1，2）知|a|＝
∵θ∈[0，π]，∴θ＝π．
解析
解析已在路上飞奔，马上就到！
知识点
4.已知向量a = (1，一 1)，向量b=(-1，2)，则(2a +b）• a = （ ）
A-
B0
C1
D2
正确答案
解析
先求出向量2a+b的坐标表示，2a+b=（1，0），然后根据向量数量积运算法则，得到（2a+b）a=1+0=1,所以选C
考查方向
本题主要考查向量的加法运算、平面向量数量积的运算律，体现了学生的基础知识掌握能力。
解题思路
先计算向量加法，再根据向量坐标计算向量数量积。
易错点
记混平面向量数量积运算律
知识点
扫码查看完整答案与解析