- 平面向量数量积的运算
- 共232题
1
题型:填空题
|
14.已知向量a=(1,

正确答案
2
解析
根据a=(1,

所以
即
考查方向
本题主要考查了平面向量的坐标运算,数量积的概念表示,向量的模的求解。
解题思路
本题考查平面向量的有关问题,
解题步骤如下:根据向量的坐标表示写出

易错点
1、向量模的求解出错;
2、向量的数量积的定义理解出错。
知识点
向量的模平面向量数量积的运算数量积表示两个向量的夹角
1
题型:填空题
|
14.在直角梯形中










正确答案
5
解析
由题可知,以A为原点建系,

F(1/λ,√3),所以
考查方向
本题主要考查平面几何与平面向量的知识
解题思路
1、画出平面图形并利用坐标系分析;2、表示平面向量,即可得到结果。
易错点
本题易在表示平面向量时发生错误。
知识点
向量的线性运算性质及几何意义平面向量数量积的运算向量在几何中的应用
1
题型:
单选题
|
10. 在边长为2的正三角形ABC中,D为BC中点,点P是该等边三角形的三边上的动点,求
正确答案
A
解析
设AD的中点为O,那么

考查方向
本题主要考查了平面向量基本知识以及运动变化和函数的思想,平面向量是高考中重要的一个考点,是每年必考的,其中数量积也是高频考题。
解题思路
本题可以建立坐标系用向量建立函数关系,可以直接用向量点积的几何意义建立函数关系求解
易错点
容易选择D答案,选择两个端点检验。
知识点
三角形中的几何计算平面向量数量积的运算向量在几何中的应用
1
题型:
单选题
|
4.设向量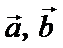
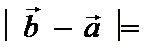
正确答案
A
解析

考查方向
本题主要考查平面向量的点积
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
向量的模平面向量数量积的运算
1
题型:填空题
|
12. 已知向量



正确答案
解析
考查方向
本题主要考察了向量的数量积运算
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
平面向量数量积的运算数量积表示两个向量的夹角数量积判断两个平面向量的垂直关系
下一知识点 : 数量积表示两个向量的夹角
扫码查看完整答案与解析