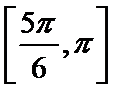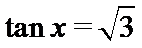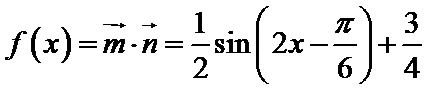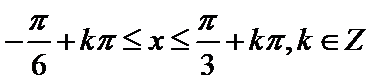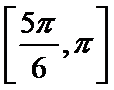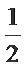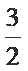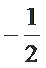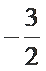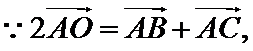- 平面向量数量积的运算
- 共232题
13.已知向量




正确答案
6
解析
考查方向
解题思路
直接利用向量数量积的运算律求解即可。
易错点
不会向量的知识,意将
知识点
4. 若



正确答案
解析
设





考查方向
解题思路
由已知先条件再结合夹角公式即可算出。
易错点
公式记错。
知识点
17.已知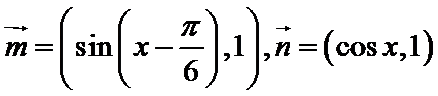
(1)若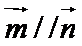
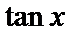
(2)若函数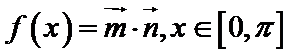
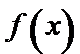
正确答案
(1)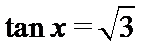
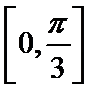
解析
试题分析:本题属于向量结合三角函数的问题,题目的难度是逐渐由易到难,
(1)直向量共线的坐标表示可以解出,
(2)先将函数求出来再化简最终可以得到单调增区间。
(1)由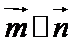
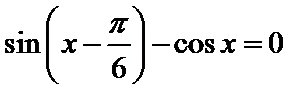
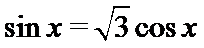
即
(2)
由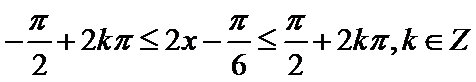
又因为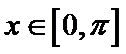
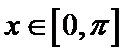
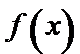
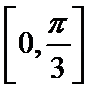
考查方向
解题思路
本题考查向量和三角函数的综合应用,解题步骤如下:由向量共线的坐标表示可以解出第一问,第二问先将函数求出来再化简最终可以得到单调增区间。
易错点
不知道怎么化简。
知识点
4.向量


正确答案
解析
由










考查方向
解题思路
先根据题意得到

易错点
不会根据

知识点
10.已知点P是函数y=sin(2x+θ)图像与x轴的一个
交点,A,B为P点右侧同一周期上的最大值和最小
值点,则

正确答案
解析
可以考虑特殊情况,即当θ=0时来做,故p可以选择原点,AB两点的坐标也很容易表示出来,所以利用向量的数量积的坐标运算可得


考查方向
解题思路
可以找一种特殊情况来做。
易错点
不会求其数量积。
知识点
7.已知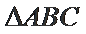
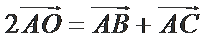
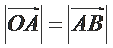
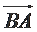
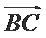
正确答案
解析
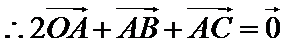
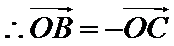
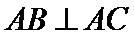
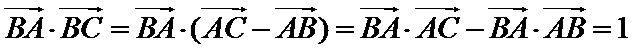
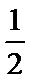
考查方向
解题思路
利用向量的运算法则将已知等式化简,对三角形的形状进行探究,利用运算法则展开求出投影,选出正确的选项
易错点
计算错误
知识点
5. 已知不共线的两个向量



正确答案
解析
将已知的2个式子左右同时平方再相减即可得
【修改点】将已知

考查方向
解题思路
由垂直数量积为0得一个式子,由已知的模左右同时平方得一个式子,两式联立即可解出。
易错点
模的计算方法不清楚。
知识点
14.已知|






正确答案
解析
因为

考查方向
解题思路
先根据向量的数量积的定义,再根据向量垂直的性质求λ的值
易错点
平面向量及其应用
知识点
13.已知




正确答案

解析
试题分析:根据向量数量积的定义求出向量的夹角,再利用题中给出的条件求出
∵











故答案为:
考查方向
解题思路
根据数量积得出

易错点
向量数量积的公式的应用.
知识点
7.已知非零向量


正确答案
解析
由已知可得





考查方向
解题思路
本题考查向量的数量积运算与向量夹角之间的关系,采用两向量垂直时其数量积为零来进行转化.本题属于基础题.
易错点
注意运算的准确性
知识点
扫码查看完整答案与解析