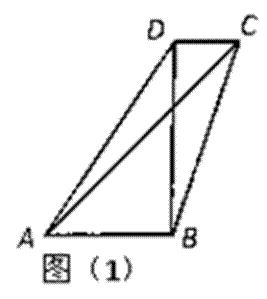
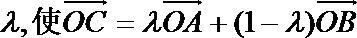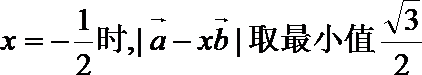- 平面向量数量积的运算
- 共232题
22.定义非零向量






(1)已知

(2)求(1)中函数
(3)已知点







正确答案
(1)



(2)


(3)

其中
当




令
当
解析
解析已在路上飞奔,马上就到!
知识点
14.已知向量






正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
18.设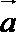
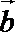
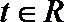
(1)记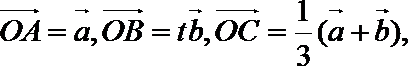
(2)若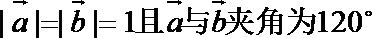
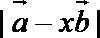
正确答案
解:(1)A、B、C三点共线知存在实数
即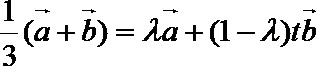
则
(2)
当
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知A,B,C是△ABC的三内角,向量
(1)求角A;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,平行四边形ABCD中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:向量




(1)若


(2)若



正确答案
(1)∵

①若





②若





(2)∵

∴ 


∴|






∴
解析
解析已在路上飞奔,马上就到!
知识点
7. 在△ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知:向量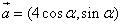
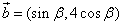
(1)若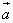
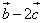
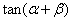
(2)求:
(3)若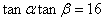
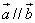
正确答案
(1)由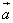
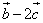
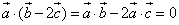
即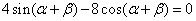
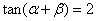
(2)
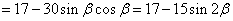
最大值为32,所以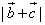
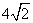
(3)由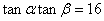
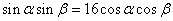
即 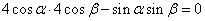
所以
解析
解析已在路上飞奔,马上就到!
知识点
15.如图(1),在四边形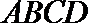
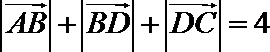
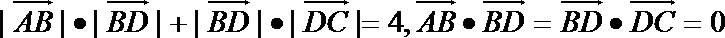
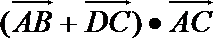
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析