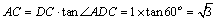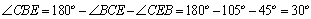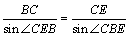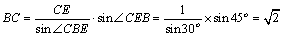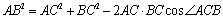- 平面的概念、画法及表示
- 共23题
如图所示,






(1)设






(2)当

正确答案
(1)


解析
(1)由△NDC∽△NAM,可得
∴

故
由




故所求函数的解析式为

(2)令


故



当且仅当





故当



知识点
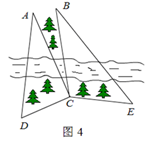
如图4,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据: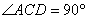
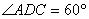
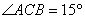
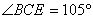
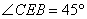
(1)求△CDE的面积;
(2)求A,B之间的距离.
正确答案
见解析。
解析
(1)连结DE,在CDE中,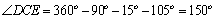
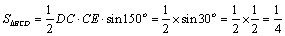
(2)依题意知,在RTACD中,
在BCE中,
由正弦定理
得
∵
在ABC中,由余弦定理
可得
∴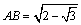
知识点
如图,在底面为直角梯形的四棱锥






(1)求证:
(2)求直线

(3)设点





正确答案
见解析
解析
(1)在直角梯形ABCD中,
所以

又因为


所以
(2)如图,在平面ABCD内过D作直线DF//AB,交BC于F,分别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系.
由条件知A(1,0,0),B(1,
设

由(1)知

设
则



(3)由(2)知C(-3,




而


…………10分
设





由
∴
知识点
如图6,已知四边形




(1)若


(2)求二面角
正确答案
见解析。
解析
知识点
如图所示,在棱长为2的正方体




中点。
(1)求异面直线

(2)求三棱锥
正确答案
(1)
解析
(1)连




可得




在正方体





在



∴

所以异面直线EF与BC所成的角为
(2)在正方体




可知



∴




又
故
所以三棱锥
知识点
在平行四边形


正确答案
解析
略
知识点
已知在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点。
(1)求证:AF∥平面PEC;
(2)求二面角P﹣EC﹣D的余弦值;
(3)求点B到平面PEC的距离。
正确答案
见解析。
解析
(1)证明:因为PA⊥平面ABCD,底面ABCD是矩形,所以以A为原点,如图建立直角坐标系。
则A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),E(1,0,0),F(
取PC的中点M,连结ME,则M(


故
(2)设平面PEC的法向量为

则

则
取平面ABCD的一个法向量为


所以二面角P﹣EC﹣D的余弦值等于
(3)

所以点B到平面PEC的距离d=
知识点
在平行四边形




正确答案
-3
解析
略
知识点
在四边形ABCD中,


正确答案
解析
略
知识点
如图,在四棱锥





(1)点





(2)在(1)的条件下,若平面

正确答案
见解析。
解析
(1)当

下面证明:若



由









(2)由PA=PD=AD=2, Q为AD的中点,则PQ⊥AD。 7分
又平面PAD⊥平面ABCD,所以PQ⊥平面ABCD,连BD,四边形ABCD为菱形,
∵AD=AB, ∠BAD=60°△ABD为正三角形,
Q为AD中点, ∴AD⊥BQ 8分
以Q为坐标原点,分别以QA、QB、QP所在的直线为


设平面MQB的法向量为
可得
取z=1,解得:
取平面ABCD的法向量

则
故二面角
知识点
扫码查看完整答案与解析