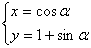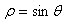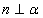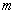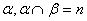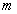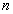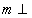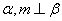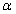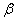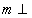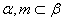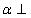平面的基本性质及推论
共22题

· 平面的基本性质及推论

平面的基本性质及推论
共22题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

如图，在四棱锥中，平面平面，且，，四边形满足，，，点分别为侧棱上的点，且。

（1）求证：平面；

（2）当时，求异面直线与所成角的余弦值；

（3）是否存在实数，使得平面平面？若存在，

试求出的值；若不存在，请说明理由。

正确答案

见解析

解析

（1）由已知，，

所以，

因为，所以。

而平面，平面，

所以平面， ……………………………………………………4分

（2）因为平面平面，

平面平面，且，

所以平面.

所以，。

又因为，

所以两两垂直， ……………………………………………………5分

如图所示，建立空间直角坐标系，

因为，，

所以

。

当时，为中点，

所以,

所以，

设异面直线与所成的角为，

所以，

所以异面直线与所成角的余弦值为。…………………………………9分

（3）设，则。

由已知，所以，

所以所以。

设平面的一个法向量为，因为,

所以即

令，得。

设平面的一个法向量为，因为,

所以即

令，则。

若平面平面，则，所以，解得。

所以当时，平面平面，…………………………………………14分

知识点

平面的基本性质及推论

题型：填空题

填空题 · 4 分

在直角坐标系中，曲线C参数方程为为参数），.点为曲线C上任一点，点满足，若以为极点，以轴正半轴为极建立极坐标系，则点所在曲线的极坐标方程为__________ 。

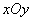
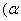
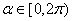
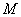
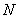
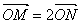
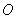
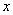
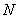
正确答案

解析

略

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

已知是平面，是直线，则下列命题中不正确的是（）。

A若∥，则

B若∥，则∥

C若，则∥

D若，则

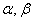
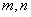
正确答案

解析

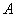
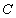
如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面，所以正确；如果两个平面与同一条直线垂直，则这两个平面平行，所以正确；

如果一个平面经过了另一个平面的一条垂线，则这两个平面平行，所以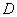也正确；

只有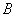选项错误，答案：。

知识点

平面的基本性质及推论

题型：简答题

简答题 · 13 分

如图，在直角坐标系中，角的顶点是原点，始边与轴正半轴重合，终边交单位圆于点，且，将角的终边按逆时针方向旋转，交单位圆于点，记。

（1）若，求；

（2）分别过作轴的垂线，垂足依次为，记△ 的面积为，△的面积为。若，求角的值。

正确答案

（1）

（2）

解析

（1）解：由三角函数定义，得，。 ………………2分

因为，，

所以。 ………………3分

所以。 ………………5分

（2）解：依题意得，。

所以， ………………7分

， ……………9分

依题意得，

整理得。 ………………11分

因为，所以，

所以，即。 ………………13分

知识点

平面的基本性质及推论

题型：填空题

填空题 · 5 分

已知与为互相垂直的单位向量，，，且与共线，则实数= 。

正确答案

解析

略

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

设是两条不同的直线，是三个不同的平面，下列命题正确的是（　）

正确答案

解析

略

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

在空间，下列命题正确的是（）

A平行直线的平行投影重合

B平行于同一直线的两个平面平行

C垂直于同一平面的两个平面平行

D垂直于同一平面的两条直线平行

正确答案

解析

由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案。

知识点

命题的真假判断与应用平面的基本性质及推论平行公理

题型：简答题

简答题 · 14 分

如图，在三棱拄中，侧面，已知

（1）求证：；

（2）试在棱(不包含端点上确定一点的位置,使得；

（3）在（2）的条件下,求二面角的平面角的正切值.

正确答案

见解析。

解析

（1）因为侧面，故

在中，由余弦定理有

故有

而且平面

（2）由

从而且故

不妨设，则，则

又则

在中有从而（舍负）

故为的中点时，

法二：

以为原点为轴，设，则由得即

化简整理得或

当时与重合不满足题意

当时为的中点

故为的中点使

（3）

取的中点，的中点，的中点，的中点

连则，连则，连则

连则，且为矩形，

又故为所求二面角的平面角

在中，

法二：由已知，所以二面角的平面角的大小为向量与的夹角

因为

故

知识点

平面的基本性质及推论

题型：单选题

单选题 · 5 分

如图，是圆的直径，是圆上的点，，，，则的值为

正确答案

解析

设，建立如图所示坐标系，则，

，，故。

知识点

平面的基本性质及推论

题型：简答题

简答题 · 12 分

如图，在斜三棱柱中，点、分别是、的中点，平面.已知，.

（1）证明：平面；

（2）求异面直线与所成的角；

（3）求与平面所成角的正弦值。

正确答案

见解析。

解析

解法一：

（1）证明：∵点、分别是、的中点，

∴ ，又∵平面，平面，

∴平面。

（2）∵平面，∴，又∵，且，

∴平面,∴。

又∵， ∴四边形为菱形，

∴，且∴平面,

∴，即异面直线与所成的角为。

（3）设点到平面的距离为，∵，

即△。

又∵在△中，,∴△。

∴，∴与平面所成角的正弦值。

解法二：

如图建系，，

，

。

（1）∵，，∴，即，

又∵平面，平面，∴平面。

（2）∵，，∴，即∴，

∴异面直线与所成的角为。

（3）设与平面所成角为，∵，

设平面的一个法向量是

则即

不妨令，可得，

∴，

∴与平面所成角的正弦值。

知识点

平面的基本性质及推论

继续学习学习下一知识点

下一知识点 : 平行公理

百度题库 > 高考 > 理科数学 > 平面的基本性质及推论

扫码查看完整答案与解析