热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

5.某工厂对新研发的一种产品进行试销，得到如下数据表：

根据上表可得回归直线方程，其中，那么单价定为元时，可预测销售的件数为（）

正确答案

解析

由表格知，那么，当x=8.3时。因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查了对线性回归方程的理解，考查考生分析和处理数据的能力。

解题思路

通过表格算出，的值，从而得到的值，再将x=8.3代入到计算得到y=84因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

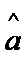
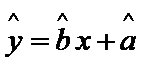
易错点

x,y任取某组给定值代入计算，从而导致出错。

知识点

线性回归方程回归分析

题型：填空题

填空题 · 5 分

调查了某地若干户家庭的年收x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，井由调查数据得到y对x的回归直线方程，由回归直线方程可知，家庭年收入每增加 1万元，年饮食支出平均增加　_________　万元。

正确答案

0.254

解析

∵对x的回归直线方程。

∴=0.254（x+1）+0.321，

∴﹣=0.254（x+1）+0.321﹣0.254x﹣0.321=0.254，

故答案为：0.254。

知识点

回归分析

题型：填空题

填空题 · 5 分

13.某次测量发现一组数据具有较强的相关性，并计算得回归方程为，其中测得的一个数据，因书写不清，只记得是内的任意一个值，则该数据对应的残差的绝对值不大于1的概率 .（残差=真实性-预测值）

正确答案

解析

求出预测值，再求出该数据对应的残差的绝对值不大于1时y0的取值范围，用几何概型解答．

考查方向

线性回归方程与几何概型

解题思路

解：由题意，预估值为　１+１＝２

该数据对应的残差的绝对值不大于１时，‍

其概率可由几何概型求得，

即该数据对应的残差的绝对值不大于１的概率：

教师点评

本题考查了几何概型的概率公式

知识点

与长度、角度有关的几何概型回归分析

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 回归分析的初步应用

百度题库 > 高考 > 理科数学 > 回归分析

扫码查看完整答案与解析