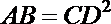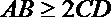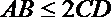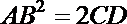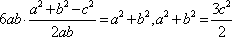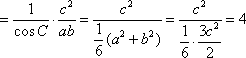- 正弦定理的应用
- 共30题
19.在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40




(1)求该船的行驶速度(单位:海里/小时)
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.直角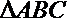
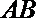
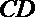
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在

已知

(1)当

(2)若角
正确答案
(1)

解析
(1)解:由题设并利用正弦定理,得
解得
(2)解:由余弦定理,b2=a2+c2-2ac cosB
=(a+c)2-2ac cosB
=p2b2-
因为


知识点
已知函数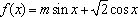
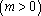
(1)求函数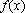
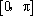
(2)已知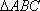
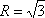
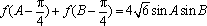
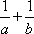
正确答案
(1)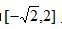
解析
(1)由题意,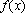
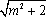
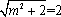
而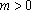
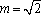
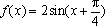
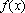
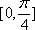
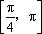
所以函数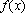
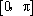
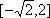
(2)化简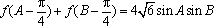
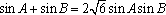
由正弦定理,得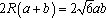
因为△ABC的外接圆半径为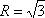
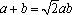
所以
知识点
在锐角三角形ABC,A、B、C的对边分别为a、b、c,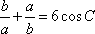
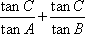
正确答案
4
解析
考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: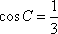
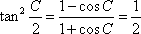
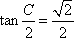
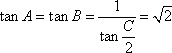
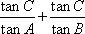
(方法二)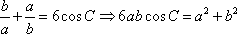
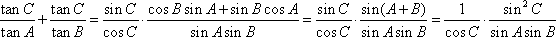
知识点
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知
(1)求角C的大小;
(2)若
正确答案
(1)
解析
(1)由题得
即
由


即
(2)



由



所以,△ABC的面积为
知识点
在





正确答案
60°
解析
解法1:由已知AD=2,∠ADE=60°,得DE=1,AE=
因为





又EC=

因此
解法2:由已知AD=2,∠ADE=60°,得DE=1,AE=
因为




所以




根据余弦定理得
因此
知识点
设





(1)求实数

(2)
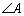




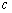



正确答案
见解析。
解析
(1)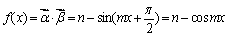
因为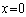
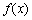
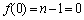
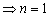
易知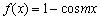

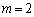

(2)由(Ⅰ)可知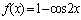
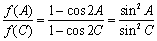
由正弦定理及余弦定理有: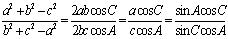
故
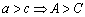
于是
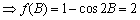
知识点
19. 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(a-c) 
(1)求角B的大小;
(2)若|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析