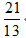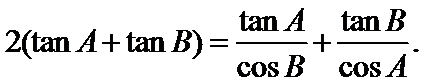· 解三角形

· 正弦定理的应用

正弦定理的应用
共30题

· 解三角形

· 正弦定理的应用

正弦定理的应用
共30题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 5 分

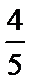
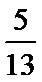
13.△ABC的内角A、B、C的对边分别为a、b、c，若cos A=，cos C=，a=1，则b= .

正确答案

知识点

正弦定理的应用余弦定理的应用

1

题型：简答题

|

简答题 · 12 分

17.△ABC的内角A，B，C的对边分别别为a，b，c，已知

（I）求C；

（II）若的面积为，求△ABC的周长．

正确答案

解（Ⅰ）∵2cos C（acosB+bcosA）=C

∴2cos C（sinAcos B+sinBcosA）=sinC

∴2cosC sin(A+B)=sinC

∴2cosC sinC=sin C

∴ 0＜C＜π

∴ cosC=

∴ C=

(Ⅱ) ∵△ABC面积为且C=

∴即

∴（a+b）2=a2+b2+2ab=13+12=25

∵a+b=5

∴a+b+c=5+

∴ABC的周长为5+

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

1

题型：填空题

|

填空题 · 5 分

15. 已知在中，的平分线把三角形分成面积比为4:3的两部分，则 .

正确答案

1/3

解析

哈哈哈

考查方向

哈哈哈

解题思路

哈哈

易错点

哈哈哈

教师点评

哈哈哈

知识点

正弦定理的应用余弦定理的应用

1

题型：简答题

|

简答题 · 12 分

16.（本小题满分12分）

在△ABC中，角A，B，C的对边分别为a，b，c，已知

（Ⅰ）证明：a+b=2c;

（Ⅱ）求cosC的最小值.

正确答案

知识点

三角函数恒等式的证明弦切互化正弦定理的应用余弦定理的应用

1

题型：填空题

|

填空题 · 12 分

（本小题满分12分）

在△ABC中，角A,B,C所对的边分别是a,b,c,且.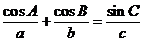

（I）证明：；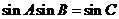

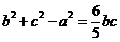
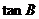
（II）若，求.

正确答案

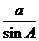
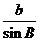
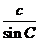
（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

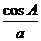
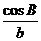
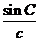
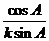
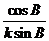
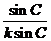
代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

（Ⅱ）由已知，b2+c2–a2=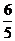bc，根据余弦定理，有

cos A==．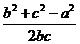

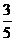
所以sin A==．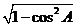

由（Ⅰ），sin Asin B=sin Acos B+cos Asin B，

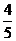
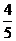
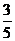
所以sin B=cos B+sin B，

故tan B=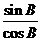=4．

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 余弦定理

百度题库 > 高考 > 理科数学 > 正弦定理的应用

扫码查看完整答案与解析