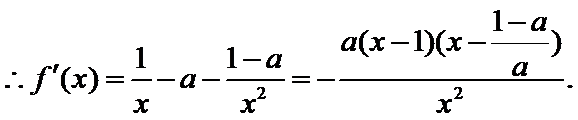- 函数的最值及其几何意义
- 共151题
21.设函数f(x)=acos2x+(a-1)(cosx+1),其中a>0,记
(Ⅰ)求f'(x);
(Ⅱ)求A;
(Ⅲ)证明
正确答案
知识点
7.函数y=2x2–e|x|在[–2,2]的图像大致为
正确答案
知识点
(本小题满分12分)
(I)讨论函数

(II)证明:当



正确答案
(Ⅰ)

且仅当



因此当
所以
(II)
由(I)知,
因此,存在唯一


当

当

因此

于是

所以,由
因为

使得

综上,当



知识点
14.设函数
①若

②若

正确答案
(1)1,(2)

解析
①







(2)①若函数









②若函数




















考查方向
解题思路
本题考点为函数的有关性质,涉及函数图象、函数的最值,函数的零点、分类讨论思想解题.利用函数图象研究函数的单调性,求出函数的最值,涉计参数问题,针对参数进行分类讨论.
知识点
14.设函数






正确答案
解析
根据条件知P, Q的横坐标互为相反数,不妨设P(-t, t3+t2), B(t, f(t)(t>0)
若t<e,则f(t)=-t3+t2,
由∠POQ是直角得
即t4-t2+1=0.此时无解;
若t≥1,则f(t)=alnx,.由于PQ的中点在y轴上,且∠POQ是直角,
所以Q点不可能在x轴上,即t≠1.
同理
整理后得 实数a的取值范围是
考查方向
解题思路
利用垂直的条件即数量积为0是本题破题的关键,同时对变量进行分类讨论,转化为求函数的值域问题。
易错点
1、

2、分类讨论的标准,如何不重复、不遗漏。
知识点
已知函数f(x)=lnx-ax+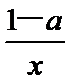
25.求函数f(x)的单调递增区间;
26.当a∈(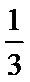
正确答案
(1)a≤0时,单调递增区间为(1,+∞);0<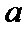
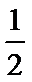
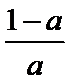
a=
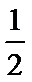
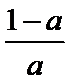
a>1时, 单调递增区间为(0,1).
解析
解:(1)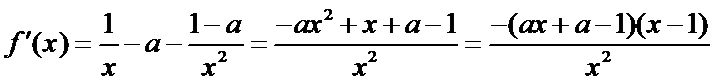
令
当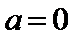
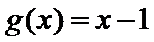
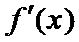
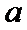
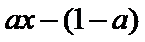
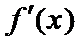
当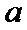
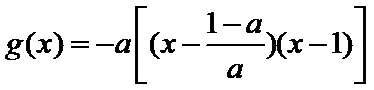
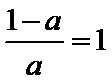
当0<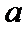
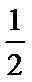
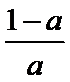
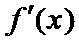
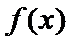
当a= 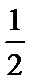
当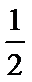
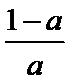
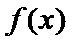
当a>1时,x∈(0,1)时,f'(x)>0,f(x)单调递增.
综上所述, a≤0时,单调递增区间为(1,+∞);
0<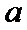
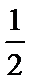
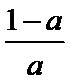
a=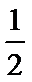
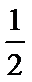
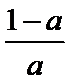
a>1时, 单调递增区间为(0,1).
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
正确答案
(2)
解析
解:
(2)由题知函数
①当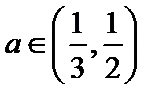
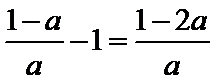
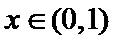
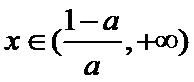
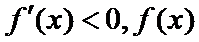
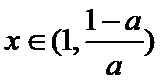
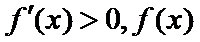
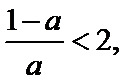
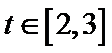
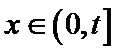
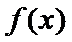
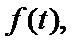
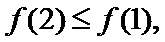
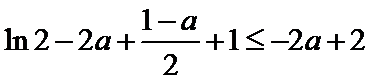
②当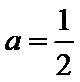
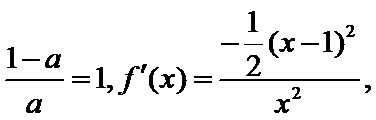
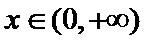
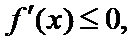
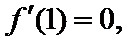
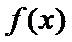
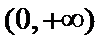
③当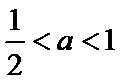
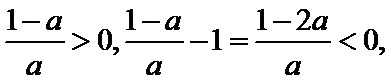
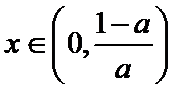
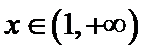
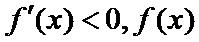
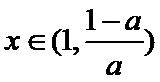
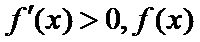
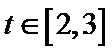
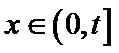
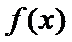
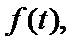
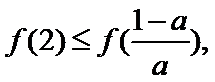
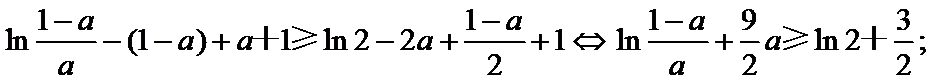
所以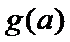
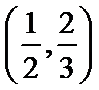
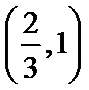
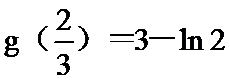
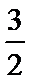
综上所述: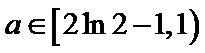
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
已知函数

27. 讨论
28. 设曲线




29. 若关于


正确答案
(I) 当









解析
(I)解:由






下面分两种情况讨论:
(1)当
令


当


-
+
-
所以,




当


当


所以,


考查方向
解题思路
利用导数的运算、导数的几何意义解答。
易错点
不会分类讨论。
正确答案
(II)见解析;
解析
(II)证明:设点










由于















考查方向
解题思路
利用导数研究函数的性质、证明不等式等基础知识和方法.
易错点
不会利用导数的几何意义来解答。
正确答案
(III)见解析.
解析
(III)证明:不妨设








类似地,设曲线






设方程






由此可得
因为


所以,
考查方向
解题思路
分类讨论思想、函数思想和划归思想,综合分析问题和解决问题的能力。
易错点
难度大做不出来。
21. 已知函数
(I)

(II)当



(III)若关于



正确答案
(1)1;
(2)2
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.
(I)当

所以函数

又因为

(II)函数

当
令

所以

当


所以


当










而

当



所以



不合题意 综上可得
(III) 因为方程










由





∴


满足
两式相加得:




即证
设

则



∴

考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,算极值。2、构造



易错点
1、第二问中的易丢对a的分类讨论。
2、第三问中构造函数不正确得不到正确结论。
知识点
已知函数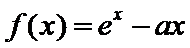
25.当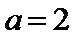
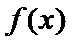
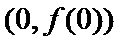
26.在25题的条件下,求证: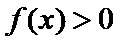
27.当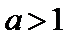
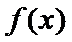
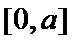
正确答案
见解析
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
当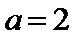
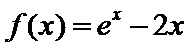
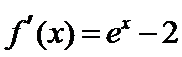
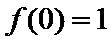
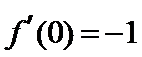
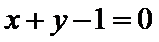
考查方向
解题思路
利用导数的几何意义求切线方程;
易错点
第三问对题中所给条件不知如何下手导致失分。
正确答案
见解析
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
由25题知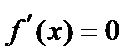

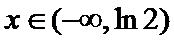
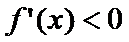

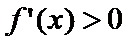
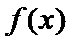
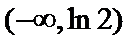
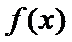
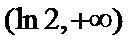
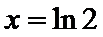
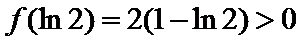
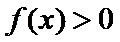
考查方向
解题思路
利用单调性进行证明;
易错点
第三问对题中所给条件不知如何下手导致失分。
正确答案
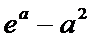
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
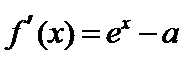
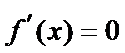
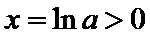
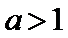
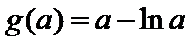
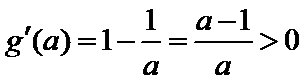
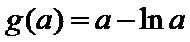
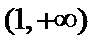

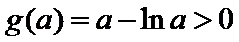
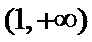
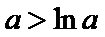
当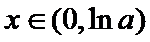
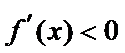
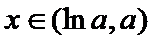
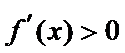
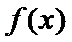
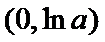
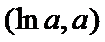
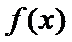
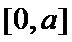
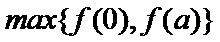
因为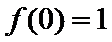

设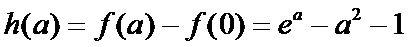
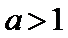
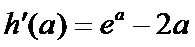
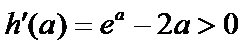
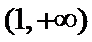
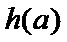
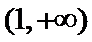
又因为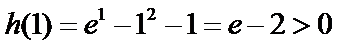
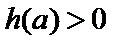
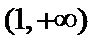
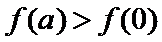
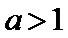
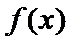

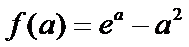
考查方向
解题思路
利用函数的单调性求最值.
易错点
第三问对题中所给条件不知如何下手导致失分。
15.某房地产公司要在一块矩形宽阔地面(如图)上开发物业 ,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线



正确答案
解析
根据题意,当开发面积最大时,三角形OMN的面积就最小。设直线MN与曲线相切于点T




令




当且仅当




考查方向
解题思路
先设切点的坐标,并运用导数得出切线方程,再求出直线的横纵截距,最后运用基本不等式求出最值。
易错点
本题易在利用基本不等式求最值或用导研究函数最值时发生错误 。
知识点
扫码查看完整答案与解析