- 函数的最值及其几何意义
- 共151题
20.函数





(1)求

(2)求

(3)若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数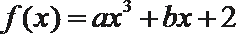
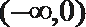
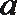
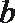
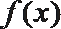
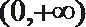
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司
(1)下列几个模拟函数中




①
③

(2)若人均GDP为1千美元时,年人均


(3)因为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知


正确答案

解析
知识点
22.请在第22、23、24三题中任选一题作答。
22.选修4-1:几何证明选讲
如图,D,E分别为


(I)证明:C,B,D,E四点共圆;
(II)若

23.选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线




(I)求
(II)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线


24.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析








