- 奇函数
- 共13题
已知函数



若


正确答案
解析
由





由①②得


知识点
若奇函数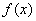
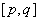
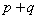
正确答案
0
解析
略
知识点
已知函数




(1)证明函数
(2)求数列{
(3)令


正确答案
见解析
解析
(1)解:由于对任意
令
解得
令

∴函数
(2)解:先用数学归纳法证明
①当n=1时

②假设n=k时,结论成立,即
当
又
即
由①②知对任意
求数列
法一:
∵函数

∴数列

∴数列

法二:

∴数列

∴数列

(3)证法一:由(2)知

当






∴当

∴当

证法二:由(2)知





下面用数学归纳法证明不等式
①当n=2时,左边
∴n=2时,不等式成立.
②假设

则n=k+1时,
左边



由①②知,当

证法三:由(2)知


由于对任意x>0,y>0,有

于是对



故


知识点
一个盒子装有六张卡片,上面分别写着如下六个函数:





(1)从中任意拿取
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
正确答案
见解析。
解析
(1)





所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,
一个为偶函数;故基本事件总数为
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为
故所求概率为
(2)


故


知识点
若










正确答案
解析
略
知识点
扫码查看完整答案与解析










































