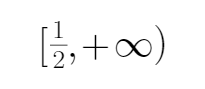- 函数的最值及其几何意义
- 共151题
20.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当




②当
当且仅当

综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知





(1)若


(2)设





正确答案
(1)“







(2) 当
对任意






由


解析
解析已在路上飞奔,马上就到!
知识点
20.设函数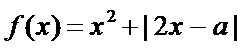
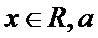
(1)若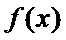
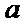
(2)设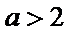
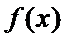
正确答案
(1)由已知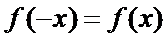
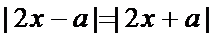
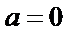
(2)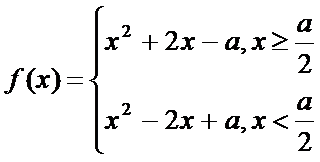
当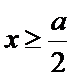
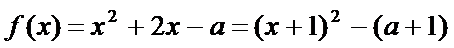
由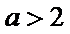
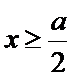
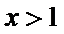
故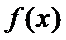
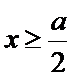
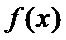
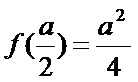
当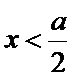
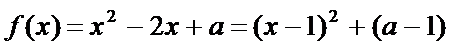
故当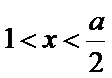
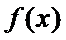
当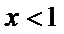
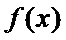
则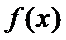
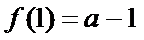
由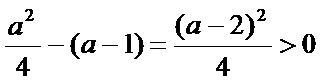
知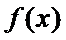
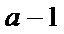
解析
解析已在路上飞奔,马上就到!
知识点
19.某化工厂生产某种产品,每件产品的生产成本是3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11-x)2万件;若该企业所生产的产品全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a(1≤a≤3)。
(1)求该企业正常生产一年的利润L(x)与出厂价x的函数关系式;
(2)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设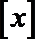
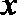
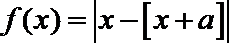
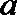
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析