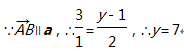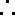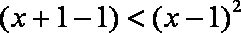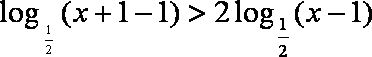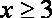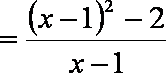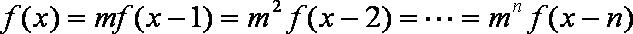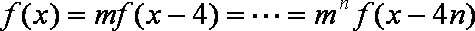- 二次函数与幂函数
- 共1316题
已知函数

(1)求
(2)求
正确答案
见解析
解析
(1)令

所以

由 


由 


综上,函数


(2)
因为

当



当



知识点
已知向量

(1)若

(2)若


正确答案
见解析。
解析
(1)由


所以
(2)由

即
又


所以
知识点
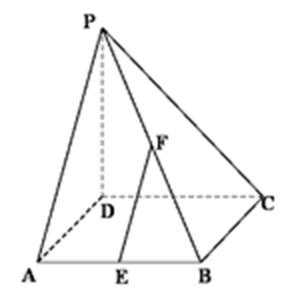
如图,设













(1)证明:

(2)证明:平面

正确答案
见解析
解析
(1)在折起后的图中,取




∵



∴

又∵



∴

∴四边形
∴
又∵



∴

(2) 在折起后的图中,∵

∴



∴
∵


又∵



∵

∵




∵

∵


∵



知识点
已知点
正确答案
解析
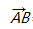
知识点
已知

(1)求
(2)若
(3)证明:
正确答案
见解析
解析
(1)


(2)由(1)知,
令
则

①当

若






②






所以
综上所述,所求的取值范围是
(3)有(2)知当


取
令


即
所以
上式中n=1,2,3,…,n,然后n个不等式相加得到
知识点
如图,在四棱锥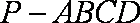
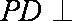
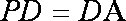
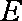
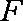
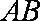
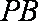
(1)求异面直线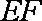
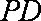
(2)当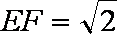
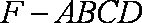
正确答案
见解析
解析
(1)∵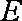
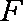
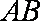
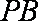
∴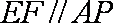
∴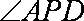
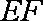
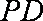
∵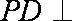
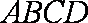
∴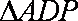
∴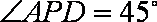
∴异面直线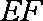
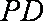
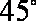
(2)由(1)知,
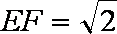
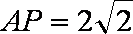
又由题意知,
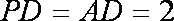
又
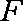
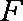
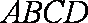
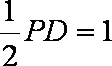
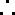
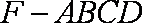
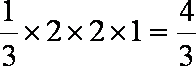
知识点
已知函数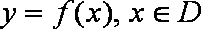
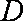
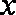
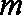
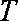
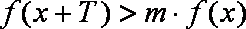
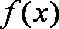
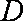
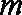
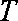
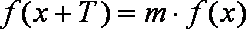
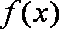
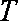
(1)试判断函数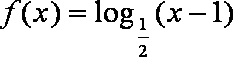
(2)已知函数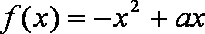
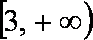
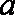
(3)下面两个问题可以任选一个问题作答,问题(Ⅰ)6分,问题(Ⅱ)8分,如果你选做了两个,我们将按照问题(Ⅰ)给你记分。
(Ⅰ)已知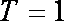
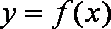
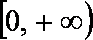
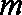
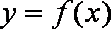
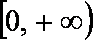
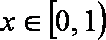
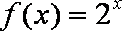
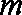
(Ⅱ)已知当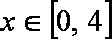
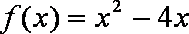
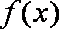
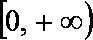
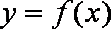

正确答案
见解析
解析
(1)∵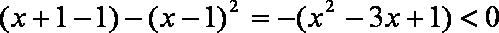
∴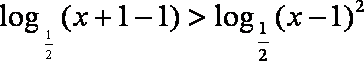
即 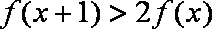
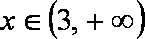
故 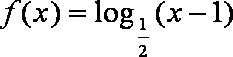
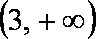
(2)由题意可知: 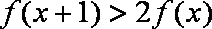
即 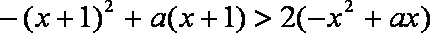
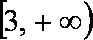
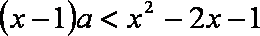
∵
∴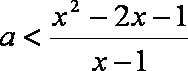
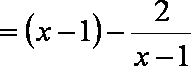
令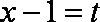
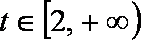
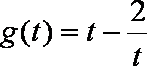
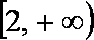
所以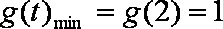
所以
(3)问题(Ⅰ)∵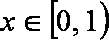
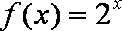
∴当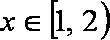
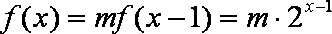
当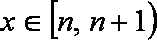
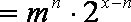
即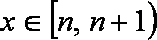
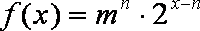
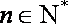
∵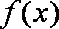
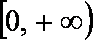
∴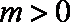
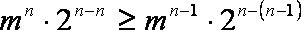
即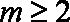
问题(Ⅱ):∵当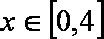
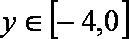
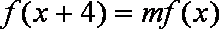
∴当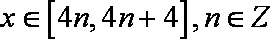
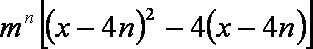
当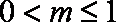
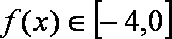
当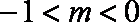

当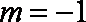
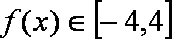
当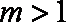
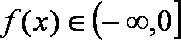
当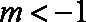
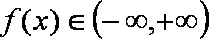
综上可知: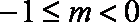
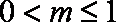
知识点
已知函数
(1)设P,Q是函数
(2)求实数


正确答案
见解析
解析
解:(1)由题意,得
所以函数
设



(2)当

当


①当


所以

所以
②当


于是
因为


所以

所以

亦即
(i)当


所以


(ii)当


当



从而

综上所述,实数

知识点
已知






正确答案
见解析
解析



由

由

∴当

当

知识点
设函数
(1)求
(2)在锐角△







正确答案
见解析。
解析
(1)
=
所以

值域为
(2)由





∵


在△ABC中,由正弦定理得
∴
知识点
扫码查看完整答案与解析