- 二次函数与幂函数
- 共1316题
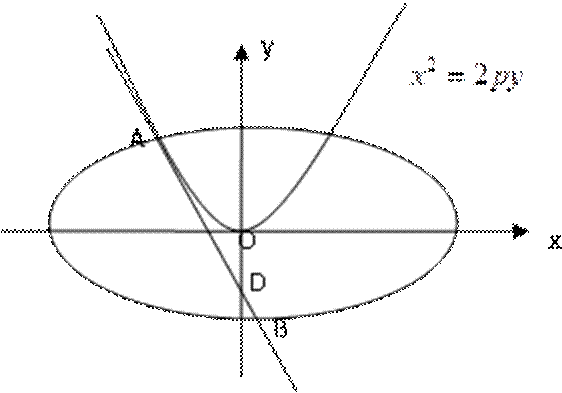
如图,已知点D(0,-2),过点D作抛物线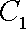
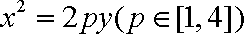
(1)求切点A的纵坐标;
(2)若离心率为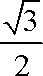
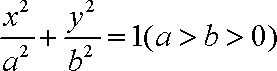
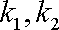
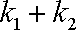
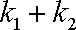
正确答案
见解析。
解析
解析:(1)设切点A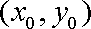
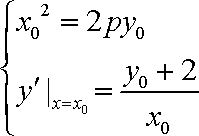
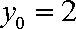
(2)依题意可设椭圆的方程为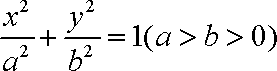
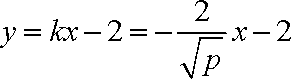
由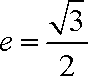
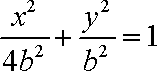
由(1)可得A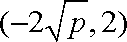
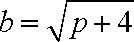
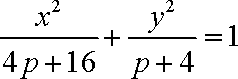
联立直线AB与椭圆的方程: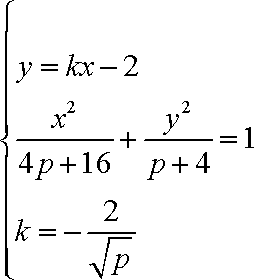
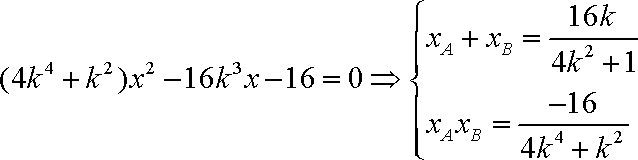
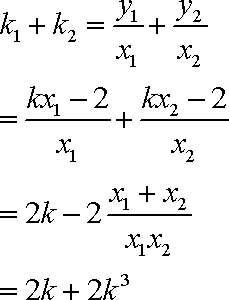
又∵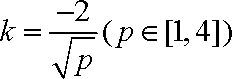
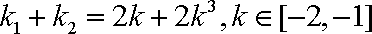
(3)由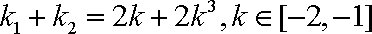
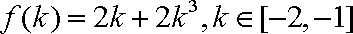
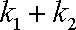
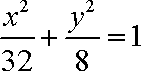
知识点
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数。
如:


已经证明:若








正确答案

解析
若




其所有正约数之和为
知识点
已知正项数列



(1)证明数列
(2)若


正确答案
见解析
解析
(1)证明:由题意知
当

当
两式相减得


由于



即数列

∴数列

(2)由(1)知



知识点
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形


(1)求V关于θ的函数表达式;
(2)求
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由。
正确答案
见解析。
解析
(1)梯形



体积
(2)
令


∵

当


当


∴当
(3)木梁的侧面积





设


∴当


又由(2)知

所以
综上,当木梁的体积V最大时,其表面积S也最大。
知识点
一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水池的长和宽,使总造价最低.
正确答案
见解析。
解析
(1)设污水处理池的宽为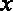
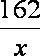
则总造价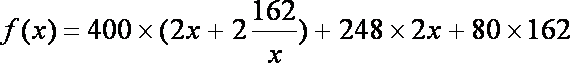
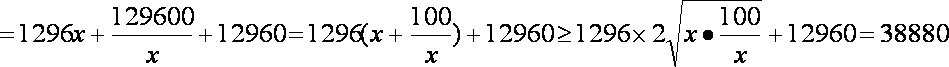
………………6分
当且仅当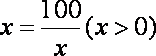

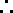
(2)由限制条件知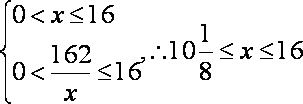
设
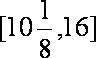
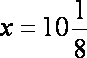

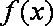
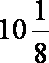
知识点
已知抛物线



(1)求抛物线

(2)过点







(3)直线










正确答案
见解析
解析
(1)由抛物线





同理由椭圆





(2)设直线


联立方程组



由
整理得:

(3)设
由



由①+②+③得
∴

知识点
设函数f(x)=log2x(0<x<5),则f(x)<1的概率为 。
正确答案
解析
∵函数f(x)=log2x(0<x<5),f(x)<1,
∴log2x<1,解得0<x<2,
根据几何概型的概率公式可得,
若从区间(0,5)内随机选取一个实数x,f(x)<1的概率为:P=

知识点
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程;
(2)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
正确答案
见解析
解析
(1)解法1:设M的坐标为

易知圆



化简得曲线

解法2:由题设知,曲线






(2)当点P在直线





于是
整理得
设过P所作的两条切线



由

设四点A,B,C,D的纵坐标分别为
所以
同理可得
于是由②,④,⑤三式得

所以,当P在直线
知识点
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系。
对某小组学生每周用于数学的学习时间

由表中样本数据求得回归方程为


正确答案
解析
样本数据的中心点为

知识点
已知函数
(1)求函数
(2)在




正确答案
见解析
解析
(1)


由


故


(2)
又

知识点
扫码查看完整答案与解析