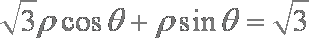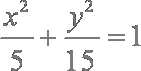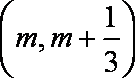- 二次函数与幂函数
- 共1316题
已知函数
(1)求f(x)的最小正周期;
(2)求f(x)在区间
正确答案
见解析。
解析
(1)化简可得
=
=
=
所以
(2)因为
所以
当

当

知识点
设函数

(1)求
(2)若






正确答案
见解析。
解析
(1)




当


当


(2)因为
即
∴
∵


∴

由余弦定理得:
∴
知识点
设

(1)当
(2)当
正确答案
见解析。
解析
(1)
由正弦定理得




由余弦定理
得4=

∴
∴
知识点
在直角坐标系中,曲线C的参数方程为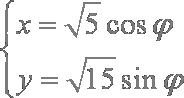
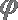
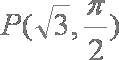

(1)判断点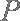
(2)设直线l与曲线C的两个交点为A、B,求
正确答案
见解析
解析
(1)直线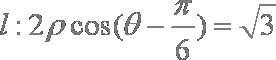


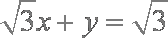

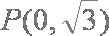
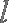
(2)直线
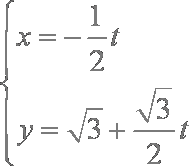
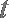
曲线C的直角坐标方程为
将直线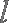
有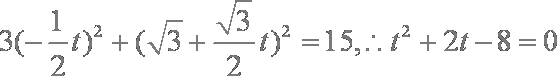
设两根为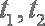
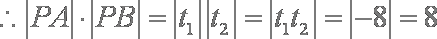
知识点
如图,






(1)求证:平面
(2)求几何体ABCDEF的体积
正确答案
见解析
解析
(1)

又

(2)因为










所以几何体的体积
知识点
已知


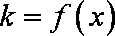
(1)若函数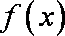

(2)设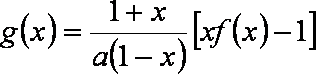
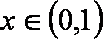
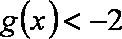

正确答案
见解析
解析
(1)由题意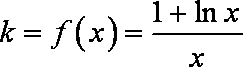
所以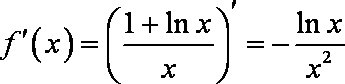
当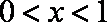


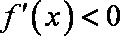


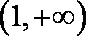
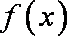
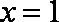
因为函数

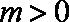
所以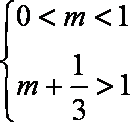
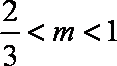


(2)由题可知,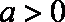
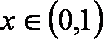

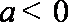
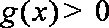
当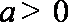
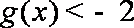


设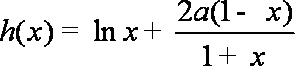
设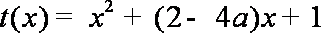
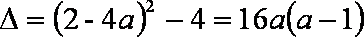
①若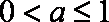
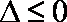

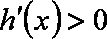
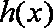
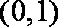
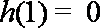

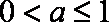
②若

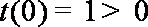


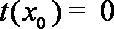
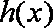
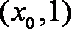
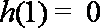
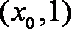
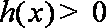
综合①②可得
知识点
抛物线y2 = 8x的焦点到双曲线 – = 1的渐近线的距离为___▲__。
正确答案
1
解析
由题意有,抛物线y2 = 8x的焦点为(2,0),双曲线的渐近线方程中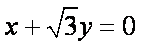
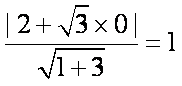
知识点
如果数列




(1)若某4阶“归化数列”
(2)若某11阶“归化数列”
(3)若

正确答案
见解析。
解析
(1)设



得




所以数列

(2)设等差数列


所以


当
当


所以
当


所以
所以
(3)由已知可知,必有ai>0,也必有aj<0(i,j∈{1,2,…,n,且i≠j)。
设

由已知得X= a+a+…+a=,Y= a+a+…+a=-。
所以
知识点
已知数列



(1)求数列
(2)设



正确答案
见解析
解析
(1) 当


当
∴


故

(2)由(1)知



故使


知识点
已知函数
(1)若



(2)若


(3)求函数

正确答案
见解析
解析
解:(1)因为


当且仅当x=2时取等号,所以

(2)由题意知,当





则由
(3)记


①当



②当a<1时,可知2a-1<a,所以
(ⅰ)当




(ⅱ)当




③当

(ⅰ)当




(ⅱ)当




(ⅲ)当



为
综上所述, 函数

知识点
扫码查看完整答案与解析