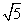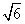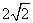二次函数与幂函数
共1316题

二次函数与幂函数
共1316题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

若函数的导函数在区间上的图像关于直线对称，则函数在区间上的图象可能是

A①④

B②④

C②③

D③④

正确答案

解析

略

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

相关变量x、y的样本数据如下表：

经回归分析可得y与x线性相关，并由最小二乘法求得回归直线方程为，则a＝

A0.1

B0.2

C0.3

D0.4

正确答案

解析

略

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

填空题 · 5 分

函数的定义域是　　。

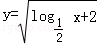
正确答案

（0，4]

解析

要使函数有意义，必有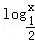+2≥0，因为0＜a＜1时对数函数是减函数，

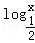
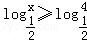
所以+2≥0可得，所以0＜x≤4

故答案为：（0，4]

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

填空题 · 4 分

当时，幂函数的图象不可能经过第象限。

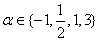
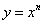
正确答案

二、四

解析

略

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

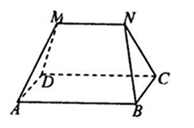
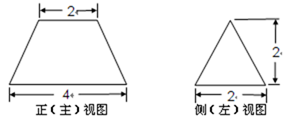
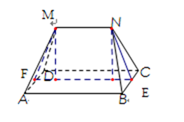
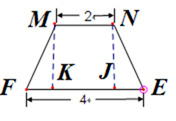
多面体MN-ABCD的底面ABCD为矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则AM的长

正确答案

解析

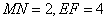
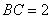
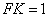
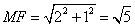
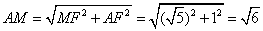
由正视图可知，由侧视图可知多面体的高为2，.所以,，所以，选C.

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 14 分

已知N，设函数R.

（1）求函数R的单调区间；

（2）是否存在整数，对于任意N，关于的方程在区间上有唯一实数解，若存在，求的值；若不存在，说明理由。

正确答案

见解析。

解析

（1）解：∵

∴.

方程的判别式.

当时，，，

故函数在R上单调递减；

当时，方程的两个实根为，

则时，；时，；时，；

故函数的单调递减区间为和，

单调递增区间为.

（2）解：存在，对于任意N，关于的方程在区间上有唯

一实数解，理由如下：

当时，，令，解得，

∴关于的方程有唯一实数解.

当时，由，

得.

若，则，

若，则,

若且时，则,

当时，,

∴，故在上单调递减.

∵，

∴方程在上有唯一实数解.

当时，；当时，.

综上所述，对于任意N，关于的方程在区间上有唯一实数解。

∴.

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

下列结论正确的是

A若向量a∥b，则存在唯一的实数使

B已知向量a，b为非零向量，则“a，b的夹角为钝角”的充要条件是“ab<0’’

C“若，则 ”的否命题为“若，则 ”

D若命题，则

正确答案

解析

略

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

等比数列共有奇数项，所有奇数项和，所有偶数项和，

末项是19，则首项（）

正确答案

解析

略

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 13 分

已知函数.

（1）讨论函数的单调性；

（2）若对任意及时，恒有成立，求实数的取值范围.

正确答案

见解析。

解析

（1） ………………………………………2分

①当时，恒有，则在上是增函数；………………………4分

②当时，当时，，则在上是增函数；

当时，，则在上是减函数 …………………6分

综上，当时，在上是增函数；当时，在上是增函数，在上是减函数. …………………………………………………7分

（2）由题意知对任意及时，

恒有成立，等价于

因为，所以

由（1）知：当时，在上是减函数

所以…………………………………………………………………10分

所以，即

因为，所以…………………………………………………12分

所以实数的取值范围为 ………………………………………………………13分

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 12 分

已知。

（1）化简；

（2）若，求。

正确答案

见解析。

解析

（1）

（2）由解得

所以

知识点

幂函数的概念、解析式、定义域、值域

继续学习学习下一知识点

下一知识点 : 指数与指数函数

百度题库 > 高考 > 文科数学 > 二次函数与幂函数

扫码查看完整答案与解析