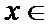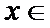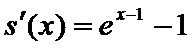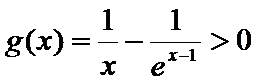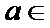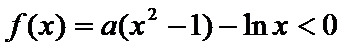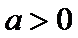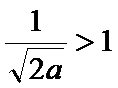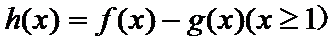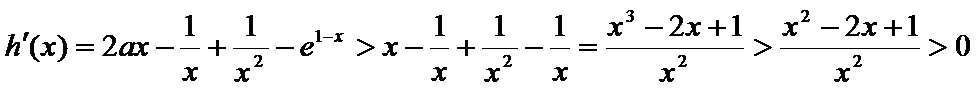- 二次函数与幂函数
- 共1316题
设函数f(x)=ax2-a-lnx,g(x)=-,其中a∈R,e=2.718…为自然对数的底数。
27.讨论f(x)的单调性;
28.证明:当x>1时,g(x)>0;
29.确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立。
正确答案
(1)当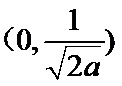
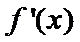
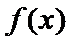
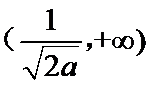
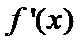
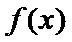
解析
(I)
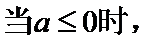
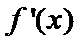
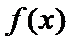
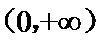
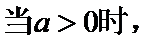
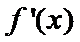
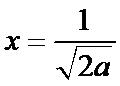
当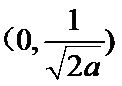
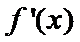
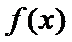
当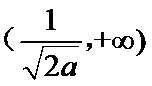
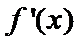
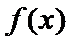
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求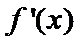
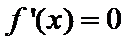
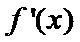
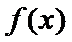
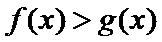
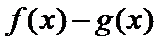
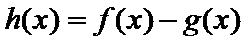
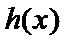
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。
正确答案
(Ⅱ)证明:令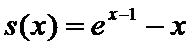
当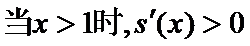
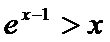
解析
(Ⅱ)证明:令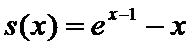
当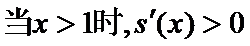
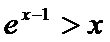
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求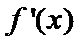
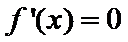
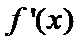
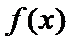
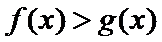
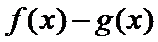
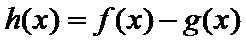
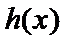
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。
正确答案
(3)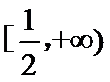
解析
(Ⅲ)由(Ⅱ)可得,当x>1时,g(x)>0;
当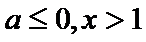
故当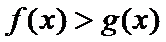
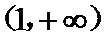
当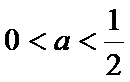
由(Ⅰ)得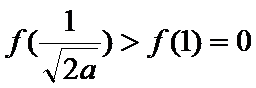
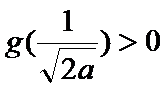
所以此时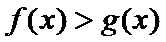
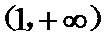
当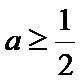
当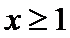
因此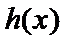
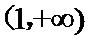
又因为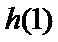
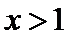
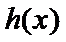
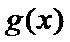
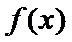
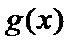
综上,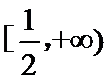
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求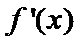
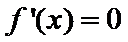
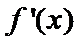
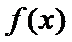
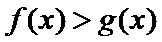
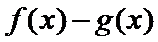
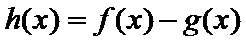
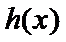
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。
7.设函数f(x)=
正确答案
3
解析
由f(-4)=f(0),得16-4b+c=c
且由对称性可知,f(x)在x=-2处取得最小值
即f(-2)=-2,得4-2b+c=-2.
联立方程解得b=4,c=2
所以f(x)=
知识点
10.若方程x2-4|x|+5-m=0恰有4个不同的实数解,则实数m的取值范围是 .
正确答案
(1,5)
解析
设函数y1=x2-4|x|+5,函数y2=m,则方程x2-4|x|+5=m的实数解就是函数y1与y2图象交点的横坐标
当方程x2-4|x|+5=m有4个不同的实数解时,两个函数的图象应有4个不同的交点,在同一直角坐标系中作出两个函数的图象,如图所示
则可得实数m的取值范围是(1,5).
知识点
4.已知函数f(x)=
正确答案
解析
f(x)=
由f(x)的图象(图略)可知f(x)在R上是单调递增函数
由f(2-a2)>f(a),得2-a2>a
即a2+a-2<0,解得-2<a<1.
知识点
9.经市场调查,某超市的一种小商品在过去的近20天内的日销售量(件)与价格(元)均为时间t(天)的函数,且日销售量近似满足g(t)=80-2t(件),价格近似满足f(t)=20-
正确答案
1225
解析
因为y=g(t)·f(t)=(80-2t)(20-
所以当0≤t≤10时,y的取值范围是[1200,1225]
在t=5时,y取得最大值为1225;
当10≤t≤20时,y的取值范围是[600,1200],
在t=10时,y取得最大值为1200.
知识点
12.已知函数f(x)=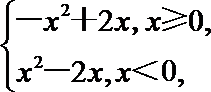
正确答案
解析
设f(x)=t,方程 t2+at-b2=0的两根分别为t1、t2,则t1t2=-b2≤0.若b≠0,则t1、t2异号,由函数图像可知,对应的x值不唯一,因此,b=0。即不等式的解为-a<t<0.注意到t=0时x=0,或x=2.因此a的最大值为8。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查分段函数和不等式
解题思路
1、画出f(x)的图像;
2、利用方程只有一个整数解求解,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在处理只有一个整数解时发生错误。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )。
正确答案
解析
由f(0)=f(4)知二次函数f(x)=ax2+bx+c对称轴为x=2,即
知识点
已知集合M={x|﹣1<x<3},N={x|﹣2<x<1},则M∩N=( )
正确答案
解析
M={x|﹣1<x<3},N={x|﹣2<x<1},则M∩N={x|﹣1<x<1}
知识点
“

正确答案
解析
略。
知识点
扫码查看完整答案与解析