- 二次函数与幂函数
- 共1316题
10.曲线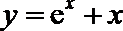
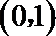
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1) 当

(2) 讨论函数
(3) 若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)当


(2)函数


(3)对于给定的正数




正确答案
(1)
由①得,


∴
(2)
当

当
综上所述,
(3)∵


当

∴
解析
解析已在路上飞奔,马上就到!
知识点
14.函数
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
10.定义在R上的函数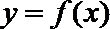
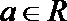
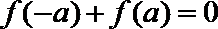
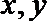
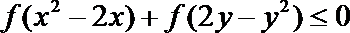
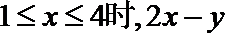
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力,加速城市之间的流通。根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次。每天来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数最多?并求出每天最多的营运人数。(注:营运人数指火车运送的人数)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知f(1sin x)=cos2x,则f(
正确答案
解析
令1-sin x=t,则t∈[0,2],所以sin x=1-t,
所以f(t)=cos2x=1-sin2x=1-(1-t)2=-t2+2t,
所以f(x)=-x2+2x(0≤x≤2),f(



知识点
4.定义在R上的函数f(x)在(-∞,2)上是增函数,且f(x+2)的图象关于y轴对称,则( )
正确答案
解析
函数f(x+2)的图象关于y轴对称,则函数f(x)关于直线x=2对称,
∵函数f(x)在(-∞,2)上是增函数,
∴函数f(x)在(2,+∞)上是减函数,
∴f(-1)=f(5)<f(4)<f(3).
知识点
扫码查看完整答案与解析