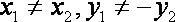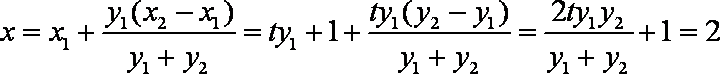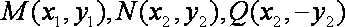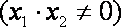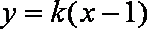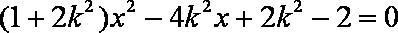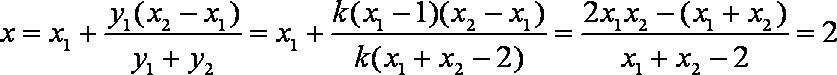- 圆的标准方程
- 共94题
已知△
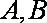
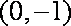
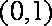
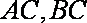
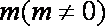
(1)求顶点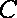
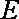
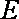
(2)当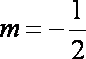
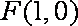
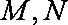
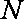
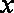
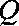
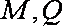
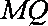
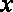
正确答案
见解析
解析
(1)由题知:
化简得: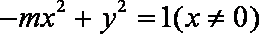
当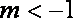
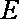
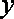
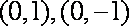
当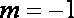
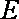
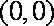
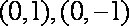
当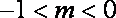
当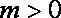
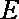
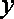
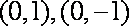
……………………6分
(2)设
依题直线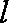
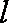
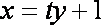
代入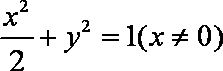
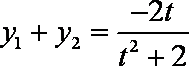
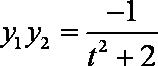
又因为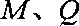
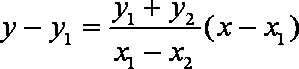
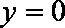
得
故直线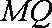
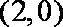
解二:设
依题直线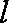
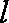
代入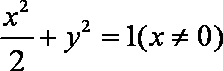
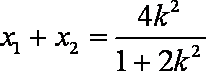
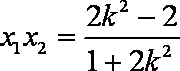
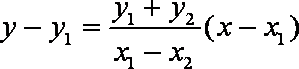
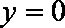
得
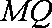
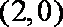
知识点
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
正确答案
见解析。
解析
建立如图所示的直角坐标系,
⊙O的方程为
直线L的方程为
(1)∵∠PAB=30°,∴点P的坐标为
∴

将x=4代入,得
∴MN的中点坐标为(4,0),MN=
∴以MN为直径的圆的方程为
同理,当点P在x轴下方时,所求圆的方程仍是
(2)设点P的坐标为



∵
将x=4代入,得



MN的中点坐标为
以MN为直径的圆

∴⊙

知识点
已知过某定圆上的每一点均可以作两条相互垂直的直线与椭圆
正确答案
解析
易得椭圆

的外接圆,方程为

垂直的直线与椭圆
知识点
已知F1、F2分别是椭圆

正确答案

解析
∵椭圆

设k=

则当|PF1|=|PF2|时,k取得最小值0;
当|PF2|=a+c=



∴k的取值范围是
故答案为
知识点
在圆

正确答案

解析
圆的半径是2,圆心






知识点
扫码查看完整答案与解析