- 圆的标准方程
- 共94题
在极坐标系中,圆


(1)求圆C的标准方程和直线
(2)若直线

正确答案
见解析
解析
(1)由
所以直线

由
又
所以,圆

(2)因为直线


两边平方得
所以a的取值范围是
知识点
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线l的参数方程为

(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值。
正确答案
见解析
解析
(1)由
所以曲线C的直角坐标方程为
(2)将直线l的参数方程代入
设A、B两点对应的参数分别为t1、t2,则
t1+t2=

∴|AB|=|t1-t2|==
当α=时,|AB|的最小值为4
知识点
在直角坐标系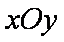
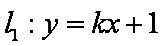
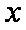
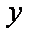
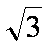
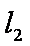
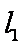
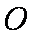
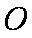
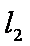
(1)求圆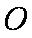
(2)圆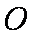
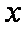
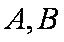
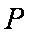
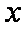

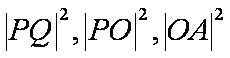
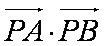
正确答案
见解析
解析
(1)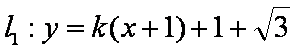
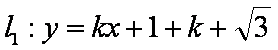
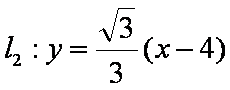
由圆O与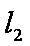
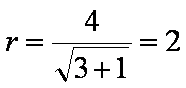
(2)不妨设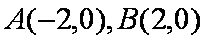
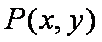
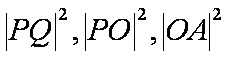
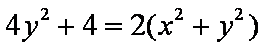
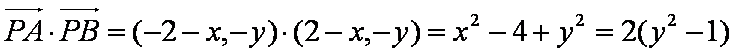
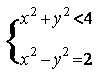
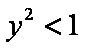
知识点
椭圆





(1)求椭圆
(2)若椭圆上两点


正确答案
见解析
解析
(1) 
将点


所以椭圆

(2)法一:设点
则

由
所以直线

法二:设点
设直线

将
得
由

所以直线

知识点
已知点


















正确答案

解析
解析:
设




将



知识点
扫码查看完整答案与解析