- 空间中直线与平面之间的位置关系
- 共30题
11.平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,

正确答案
知识点
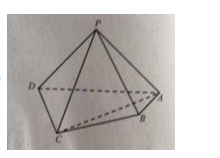
17.如图,在四棱锥P-ABCD中,平面PAD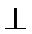
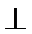
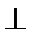
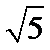
(I)求证:PD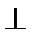
(II)求直线PB与平面PCD所成角的正弦值;
(III)在棱PA上是否存在点M,使得BM//平面PCD?若存在,求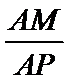
正确答案
知识点
14.α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
在四棱锥






21.证明:
22.在线段



正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
由PA⊥平面ABCD,得DE⊥PA.连接AE,因为
考查方向
解题思路
利用相关定理进行证明.
易错点
相关定理不熟容易处错。
正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:过点F作FH∥ED交AD于点H,则FH∥平面PED,且有AH=

由面面平行的判定定理可得平面GEH∥平面PFD.,进而由面面平行的性质得到EG∥平面PFD,从而确定G点位置.
考查方向
解题思路
假设平行,利用平行确定点的位置.
易错点
相关定理不熟容易处错。
5.设

①若


③若



其中命题正确序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设

①若

②若

③若

④若

其中,所有真命题的序号是( )
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
2.两个面垂直,经过第一个面内一点且垂直于交线的直线( )
正确答案
解析
因为经过第一个面内一点且垂直于交线的直线有三种情况,
分别是与第二个平面垂直、相交、平行,
所以选D.
知识点
17.对于两个平面

正确答案
解析
选项A:符合题设条件的直线

选项B:符合题设条件的直线




选项C:由图可知直线


考查方向
本题考查了空间直线与平面的位置关系,考查了空间想象能力,是容易题.
解题思路
假命题举反例即可.
易错点
符合条件的空间直线和平面的位置关系有时候并不是只有结论的这一种,空间想象能力弱的话有时候未必能想得到.
知识点
4.设a,l是直线,α和β是平面,则下列说法正确的是( )
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是简单。
考查方向
本题主要考查了线面位置关系,在近几年的各省高考题出现的频率较高。
解题思路
本题考查线面位置关系,解题步骤如下:
由题可知,A中可能l∥β;B中可能l在β内;C中可能α⊥β。
易错点
本题易在判断线是否在面上发生错误。
知识点
扫码查看完整答案与解析