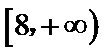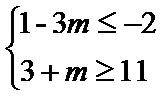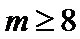- 充要条件的应用
- 共64题
7.设p:实数x,y满足(x–1)2–(y–1)2≤2,q:实数x,y满足
正确答案
知识点
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
15. 设等比数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知正方形

(1) 若正方形的一个顶点为


(2) 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设非常数数列{an}满足
(1)证明:数列{an}为等差数列的充要条件是α+2β=0;
(2)已知α=1,β=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.对于定义域为












(1)验证

(2)设



(3)证明:“







正确答案
(1)详见解析
(2)详见解析
(3)详见解析
解析
(2)由于





若







(3)若








同理,若




以下证明最后一部分结论.
由(2)所证知存在






而

类似地,当




结论成立.
知识点
14.已知p:﹣2≤x≤11,q:1﹣3m≤x≤3+m(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为_______.
正确答案
解析
¬p是¬q的必要不充分条件,
p可推出q,
可得到
解得
考查方向
解题思路
本题考查了充分条件、必要条件的判断及其在集合中的应用.充要条件转化之后,用小范围可推出大范围得到结果。
易错点
本题易在充要条件的转化过程中出错
知识点
13.设命题P:



正确答案

解析
先否定量词,后否定结论,得到的新命题是:

考查方向
解题思路
全称命题和特称命题否定的原则是否定量词、否定结论。
易错点
不理解全称命题和特称命题否定的原则而失分。
知识点
15.下列命题:①已知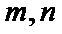
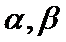
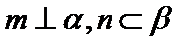
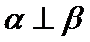
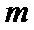
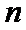
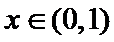
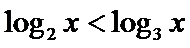
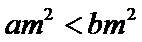
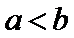
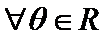
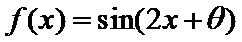
正确答案
①
解析
(1)正确(2)取x=1/2,则不等式不成立,(3)若m为0,则逆命题为假,忽略了等号,(4)当θ=π/2,时,函数为奇函数。所以答案填①
考查方向
解题思路
根据题意,逐个选项分析
易错点
相关知识点掌握不扎实
知识点
扫码查看完整答案与解析