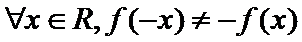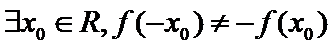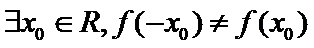- 充要条件的应用
- 共64题
1
题型:
单选题
|
5.已知命题







正确答案
B
解析




考查方向
考查复合命题及命题的真值表
解题思路
分别判断命题p,q的真假, 再分析复合命题的真假
易错点
复合命题的真值判断易出错
知识点
充要条件的判定充要条件的应用含有逻辑联结词命题的真假判断
1
题型:
单选题
|
2.若直线



正确答案
A
解析
由向量共线的定义可知,两直线平行可以得到
考查方向
向量共线。
解题思路
分别判断。
易错点
判断出错。
知识点
充要条件的应用
1
题型:填空题
|
13.若



正确答案
解析
由判别式小于等于0,即实数

考查方向
全称命题和特称命题。
解题思路
直接由判别式小于等于0即可。
易错点
不会转化。
知识点
充要条件的应用
1
题型:
单选题
|
3.设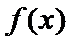
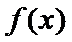
正确答案
C
考查方向
本题主要考查逆否命题的真假、奇函数的定义、全特称命题的否定等知识,意在考查考生的逻辑推理能力和转化与化归的能力。
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题;
易错点
1.全称命题的否定形式写错;2.不能正确理解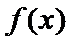
知识点
充要条件的应用函数单调性的判断与证明
下一知识点 : 命题的否定
扫码查看完整答案与解析