- 进行简单的合情推理
- 共19题
设















正确答案
解析
略
知识点
已知集合







(1)当




(2)(ⅰ)证明:若



(ⅱ)设



说明理由;
(3)记




正确答案
见解析
解析
(1)解:当

得 

由 


(2)(ⅰ)证明:设


因为 

所以 

即 


所以 

所以

(ⅱ)解:设



反例如下:取


则 



因为

所以不存在

(3)解法一:因为 
设






所以
因为 
所以 

所以 
因为

又 
所以

即 
对于 





综上,

解法二:首先证明如下引理:设

证明:因为 

所以 
即 
所以

上式等号成立的条件为


对于 





综上,

知识点
设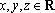
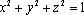


正确答案
解析
略
知识点
若存在正实数




① 



其中“在
正确答案
②③
解析
略
知识点
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似的,我们在平面向量集





①若
②若
③若

④对于任意向量
其中真命题的序号为
正确答案
解析
略
知识点
扫码查看完整答案与解析