- 众数、中位数、平均数
- 共63题
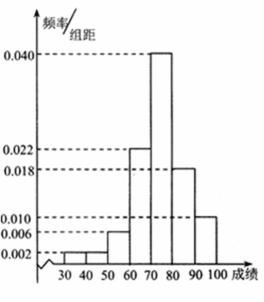
19.为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40), [40, 50), [50, 60), [60, 70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),已知测试平均成绩在区间[30,60)有20人.
(I)求m的值及中位数n;
(II)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间.根据以上抽样调查数据,该校是否需要增加体育活动时间?
正确答案
(I)由频率分布直方图知第1组,第2组和第3组的频率
分别是0.02,0.02和0.06,
则m×(0.02+0.02+0.06)=20,
解得m=200.
由直方图可知,中位数n位于[70,80),则0.02+0.02+0.06+0.22+0.04(n-70)=0.5,
解得n=74.5.
(II)设第i组的频率和频数分别为pi和xi,由图知,
p1=0.02,p2=0.02,p3=0.06,p4=0.22,p5=0.40,p6=0.18,p7=0.10,
则由xi=200×pi,可得
x1=4,x2=4,x3=12,x4=44,x5=80,x6=36,x7=20,
故该校学生测试平均成绩是
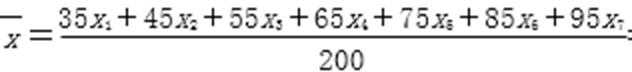
所以学校应该适当增加体育活动时间.
解析
解析已在路上飞奔,马上就到!
知识点
18.某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从抽取的6名工人中,任取2人,求恰有1名优秀工人的概率.
正确答案
解:
(1)样本均值为
(2)抽取的6名工人中2名为优秀工人,所以12名工人中有4名优秀工人.
(3)抽取的6名工人中2名为优秀工人,设为A,B;4名为非优秀工人,设为a,b,c,d
从A,B,a,b,c,d中任取2人的不同取法有
(A,B),(A,a),(A,b),(A,c),(A,d)
(B,a),(B,b),(B,c),(B,d)
(a,b),(a,c),(a,d)
(b,c),(b,d)
(c,d)共15中,其中恰有1名优秀工人的取法有
(A,a),(A,b),(A,c),(A,d),(B,a),(B,b),(B,c),(B,d)共8种
所以,恰有一名优秀工人的概率是
解析
解析已在路上飞奔,马上就到!
知识点
16. 某品牌汽车
已知分3期付款的频率为0.2,该
(Ⅰ)求上表中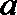
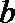
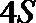
(Ⅱ)该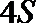
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩数据统
计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.

(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.
正确答案
解: (1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为
(2)该考场考生“数学与逻辑”科目的平均分为
(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为


设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则
解析
解析已在路上飞奔,马上就到!
知识点
9.现有10个数,其平均数是3,且这10个数的平方和是100,那么这个数组的标准差是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析