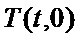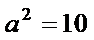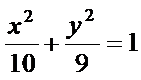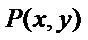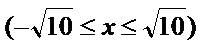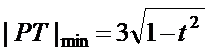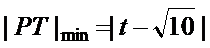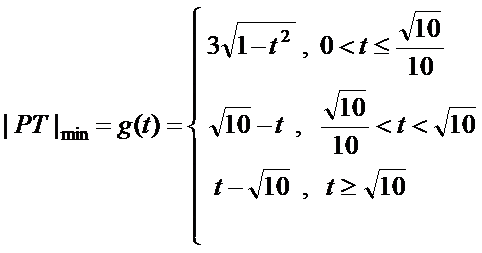圆锥曲线中的范围、最值问题
共78题

· 圆锥曲线中的范围、最值问题

圆锥曲线中的范围、最值问题
共78题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

21．已知抛物线，椭圆经过点，它们在轴上有共同的焦点，椭圆对称轴为坐标轴．

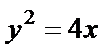
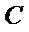
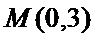
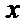
（1）求椭圆的标准方程

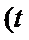
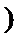
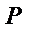
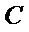
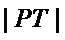
（2）设为正实数，当点在椭圆上运动时，求的最小值．

正确答案

（1）焦点，∴ ，，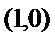

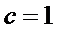
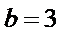
∴ 椭圆的方程为

（2）设

∴

当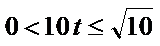时，

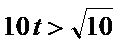
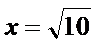
当时，，

∴

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 5 分

12．如图:切⊙O于点，，过圆心，且与圆相交于、两点，，则圆O的半径为___________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 14 分

21．已知点P（4，4），圆C：与椭圆E：有一个公共点A（3，1），F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．

（1）求m的值与椭圆E的方程；

（2）设Q为椭圆E上的一个动点，求的取值范围．

正确答案

（1）点A代入圆C方程，得．∵m＜3，∴m＝1

圆C：．设直线PF1的斜率为k，则直线PF1的方程为：，

即．∵直线PF1与圆C相切，∴．解得．

当k＝时，直线PF1与x轴的交点F1的横坐标为，不合题意，舍去．

当k＝时，直线PF1与x轴的交点F1的横坐标为－4，∴c＝4．，

2a＝|AF1|＋|AF2|＝，，a2＝18，b2＝2．

椭圆E的方程为： 2

（2），设Q（x，y），，．

∵，即，而，∴－18≤6xy≤18

所以，的取值范围是[0，36]

的取值范围是[－6，6]．∴的取值范围是[－12，0]

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算椭圆的定义及标准方程圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 5 分

12．如图，CE为圆O的直径，PE为圆O的切线，E为切点，PBA为圆O的割线，交CE于D点，CD=2，AD=3，BD=4，则圆O的半径为 _______；PB=_______.

正确答案

4；20

解析

解析已在路上飞奔，马上就到！

知识点

圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 9 分

26．已知圆同时满足下列三个条件： ① 与轴相切；② 在直线上截得弦长为；③ 圆心在直线上，求圆的方程．

正确答案

设所求的圆与直线交于、两点，

因为圆心在直线上，所以设圆心坐标为．

又圆与轴相切，所以圆的半径．

从而圆心到直线的距离为=．

又，，

在Rt△中，由，

解得．

所以圆心的坐标为或．

故所求圆的方程为或．

解析

解析已在路上飞奔，马上就到！

知识点

圆锥曲线中的范围、最值问题

继续学习学习下一知识点

下一知识点 : 圆锥曲线的定点、定值问题

百度题库 > 高考 > 理科数学 > 圆锥曲线中的范围、最值问题

扫码查看完整答案与解析