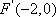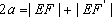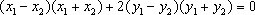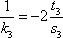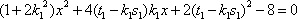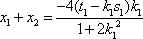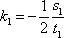- 圆锥曲线的定点、定值问题
- 共61题
给定椭圆








(1)求椭圆
(2)点




(ⅰ)当点



(ⅱ)求证:线段
正确答案
见解析
解析
(1)


准圆方程为
(2)(ⅰ)因为准圆


设过点

所以由

因为直线
所以

所以



(ⅱ)①当直线

则

当



此时



同理可证当


②当


设经过点

所以由
得
由

因为

设


所以

所以

综合①②知:因为



所以线段


所以线段
知识点
已知定点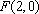
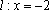
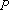

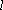
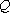
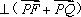

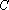
(1)求曲线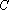
(2)过点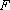

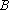
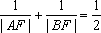
(3)记

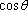
正确答案
见解析
解析
(1)设点

由题意,可得
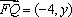
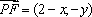
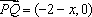
由

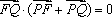
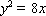
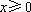
因此,所求曲线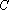
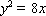
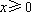
(2)因为过点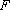
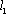
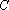

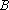

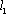
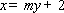
于是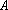
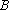
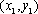
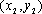
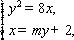
消
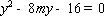
于是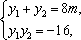

又因为曲线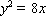
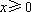

所以
(3)由(2)可知,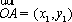
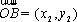
于是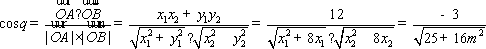
(16分)可求得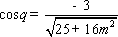
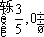
知识点
已知椭圆




(1)求椭圆
(2)已知动直线








正确答案
见解析
解析
(1)由题意知:
根据椭圆的定义得:

……………………………………3分
所以 
所以 椭圆

(2)假设在


当直线

则 
解得 
当直线

由于

下面证明

显然 直线

当直线



由




因为 

所以


综上所述:在


知识点
已知:椭圆





(1)求椭圆的方程;
(2)斜率大于零的直线过




(3)是否存在实数






正确答案
见解析
解析
(1)由



所以椭圆方程是:
(2)设EF:



设



由

得


直线


(3)将


记







解得



知识点
椭圆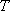

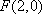
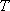
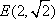
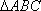
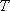
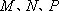
(1)求椭圆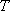
(2)设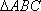
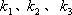
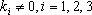
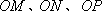
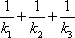
正确答案
见解析
解析
(1)设椭圆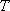

所以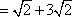
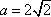
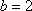
故椭圆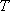
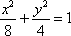
(2)设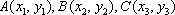
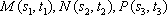
由: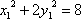
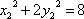
所以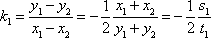
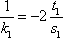
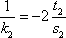
所以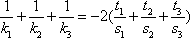
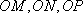
所以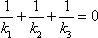
设直线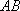
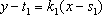
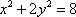
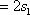
(以下略)
知识点
扫码查看完整答案与解析