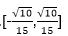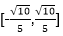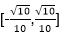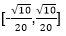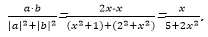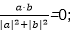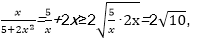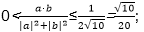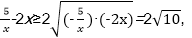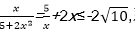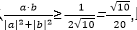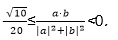不等式_章节学习

1

题型：填空题

|

填空题 · 5 分

7.设x,y均为正数,且,则xy的最小值为_________.

正确答案

49

解析

=去分母后为xy-7=3(x+y)≥6,解得xy≥49.

知识点

利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

4.若直线通过点M(cos α,sin α),则的最小值为（　　　）

A

B1

C

D

正确答案

B

解析

设向量m=(cos α,sin α),

由题意知=1,由m·n≤|m||n

可得1=

即的最小值是1,

故选B.

知识点

函数的值域利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

9.已知点P(x,y)是椭圆上的一个动点,则x-y的最小值是_______.

正确答案

解析

根据题意,令=sin θ,所以可设动点P的坐标为(θ),其中0≤θ<2π.

因此

所以当时,
x-y取最小值.

知识点

函数的值域利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

6.已知a=(x,1),b=(2,-x),那么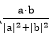的取值范围是（　　）

A

B

C

D

正确答案

D

解析

若x=0,

则

若x>0,由于

则

若x<0,由于

则

那么

即-

知识点

平面向量数量积的运算利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

7．已知a > 0，b > 0，a、b的等差中项是，且，则x + y的最小值是（）

A6

B5

C4

D3

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

4．已知，现有下列不等式：

①；

②；

③；

④，

其中正确的是（）

A②④

B①②

C③④

D①③

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用对数值大小的比较不等式的性质利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

6．各项均为正数的等差数列中，，则前12项和的最小值为（）

A

B

C

D

正确答案

D

解析

考查方向

本题主要考查等差数列的性质、求和公式，及均值不等式的应用。

解题思路

注意观察项数（下角标）的关系1+12=4+9。

易错点

无法充分利用条件，将条件引向结论。

知识点

等差数列的性质及应用利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

2．函数的值域是（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域利用基本不等式求最值

1

题型：填空题

|

填空题 · 4 分

7．若，且，则的最小值是___________．

正确答案

16

解析

∵，且

∴

（当且仅当即时，等号成立）

∴的最小值是16．

考查方向

本题考查基本不等式，是容易题．

解题思路

，展开，再利用基本不等式求得最小值，注意等号成立的条件．

易错点

当一个整数式子与一个分式式子在一个题中出现时，求一个式子的最值，常将两个式子相乘，展开，然后利用基本不等式求解．利用基本不等式求最值要注意：一正、二定、三相等．

知识点

利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

14．己知平行四边形的周长为6，则其对角线长的平方和的最小值是 .

正确答案

9

解析

本题属于平面向量和基本不等式的问题，题目的难度较小。注意转化为平面向量求解。

考查方向

本题主要考查了平面向量和基本不等式的问题。

易错点

本题必须注意转化为平面向量的问题求解，忽视则会出现错误。

知识点

利用基本不等式求最值基本不等式的实际应用

1

题型：单选题

|

单选题 · 5 分

12. 设正实数满足，则当取得最小值时，的最大值为（）

A0

B2

C

D

正确答案

B

解析

由，得，又正实数，故由均值不等式知当且仅当时取“=”号；再代回得，进而。故选B选项。

考查方向

本题主要考查了均值不等式与函数的综合是,在近几年的各省高考题出现的频率较高，属于难题。

解题思路

1、由进行代换后处理的最值问题。

2、由取等条件再把所求变成一个函数问题。

易错点

1、本题易在的代换后的处理思路上走死。

2、易忽略使用均值不等式有一个取等条件。

知识点

利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

12．在平面直角坐标系xOy中，已知，，则的最小值为

A1

B2

C3

D4

正确答案

B

解析

如图，在同一坐标系中画出函数与函数，由图像很容易知道的最小值即为曲线斜率为1的切线与直线的距离的平方。设切点为，则，解得或由知，故切线方程为，即，它与直线的距离为，所以的最小值为，故选择B选项。

考查方向

本题主要考查了数形结合思想与利用导数求曲线的切线方程,为高考常考题，在近几年的各省高考题出现的频率较高，常与函数定义域，解不等式等知识点交汇命题。

解题思路

先在同一坐标系中画出函数与函数图像，由图像很容易知道的最小值即为曲线斜率为1的切线与直线的距离的平方。

易错点

对题中条件不知如何运用导致做本题没有思路。

知识点

利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

14.若的展开式中项的系数为20，则的最小值为________．

正确答案

2

解析

因为的展开式中项的系数为20，

所以，令，所以

，所以，当且仅当时取等号，所以

的最小值为2，所以答案是2

考查方向

二次项展开式、基本不等式

解题思路

根据展开式求a和b的关系

易错点

展开式公式记错、基本不等式“一正”“二定”“三相等”

知识点

利用基本不等式求最值求二项展开式的指定项或指定项的系数

1

题型：单选题

|

单选题 · 5 分

4.设．若是与的等比中项，则的最小值为（）

A12

B24

C25

D36

正确答案

A

解析

依题意得，，

即，

所以，

即，

所以，

当且仅当2时取等号．

应选A．

考查方向

本题主要考查等比数列的定义和基本不等式的运用等内容，考查简单的运算和推理能力，难度不大。

解题思路

1.由等比数列的定义得出；

2．用基本不等式得出结果，应选A。

易错点

本题不容易想到用基本不等式推出，即，这一步。

知识点

等比数列的性质及应用利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

15. 已知函数的图象恒过定点P，若点P在直线上,其中,则的最小值为__ _____.

正确答案

解析

点P（2,2），代入直线得2m+2n=1,()(2m+2n)=4++2

考查方向

本题对数型函数的性质，均值不等式。

解题思路

先求定点坐标，代入直线得2m+2n=1,再利用均值不等式解题

易错点

“1”的应用不灵活

知识点

对数函数的图像与性质利用基本不等式求最值

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点