- 不等式
- 共1358题
函数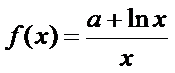
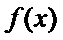

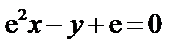
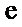

25.若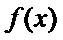
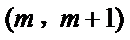


26.求证:当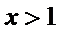
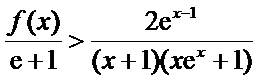
正确答案
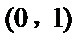
解析
因为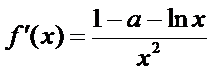
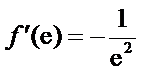
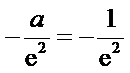
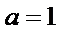
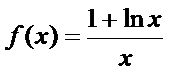
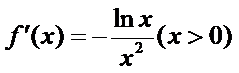
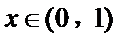
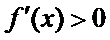
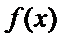
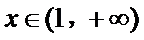
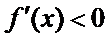
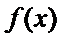
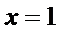
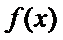
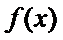
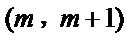
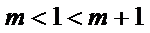
即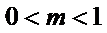
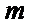
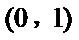
考查方向
解题思路
第一问由切线与直线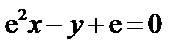
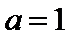
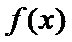
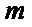
正确答案
略;
解析
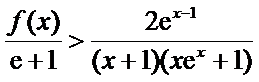
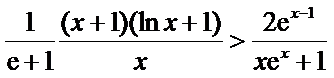
令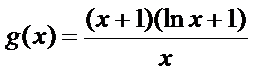
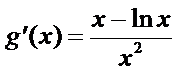
再令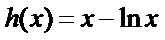
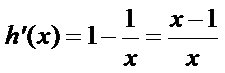
因为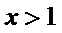
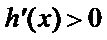
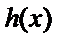
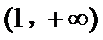
所以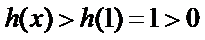
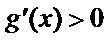
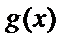
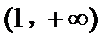
所以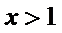
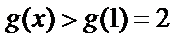

令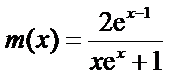

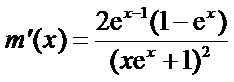
因为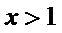
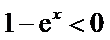
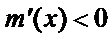
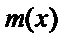
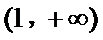
所以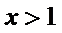
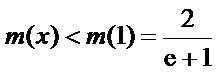
所以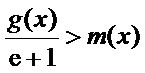
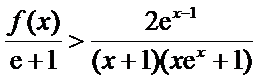
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
已知定义在R上的偶函数


25.当

26.求最大的整数



正确答案
(1)
解析
(1):当


记过原点与

则切线L斜率为
又切线过(0,0),所以



∴当



考查方向
解题思路
先设切点后利用导数的几何意义求出切点坐标后即得切线方程;
易错点
没有给出切点导致无法入手;
正确答案
(2)4
解析
(2)因为任意

当


当


∴ 

又整数


得:

∴ 

令

当


当


又


由此可见,方程


且当






下面证明:

①当




②当

令




∴

综上所述,

考查方向
解题思路
先探求出m的值后证明。
易错点
对于题中给的信息无法处理导致没有思路。
已知函数
25.若


26.若

正确答案
m=0
解析
当




只要满足

对于








对于


则

所以


所以





综上所述可得:
考查方向
解题思路
利用条件,将不等式恒成立问题转化成只要满足

易错点
利用导数在处理单调区间及分类讨论上容易出错;
正确答案
证明见解析
解析
下面用数学归纳法证明
(1)当



(2)假设


只需证明










由归纳假设

若

构造函数





故

由‚及题意知

综合


考查方向
解题思路
用分析法,从结论入手,考虑由于与正整数有关,可以用数学归纳法证明,在证明假设n=k,将












易错点
不容易考虑到用数学归纳法证明
12. 定义在




正确答案
解析
由奇函数




(1)当






(2)当




(3)当

①当



②当



③当





综上可知,

考查方向
解题思路
1.先利用奇函数求出函数在对称的区间上的单调性;
2.根据x的范围不同分类求出x的解后取并集。
易错点
1.不会奇函数在对称的区间上单调性相同这个结论;
2.分类讨论时不全或重复。
知识点
已知函数
27. 判断函数

28. 若

29.求证:
正确答案
(1)
解析
(Ⅰ)


考查方向
解题思路
直接求导后判断出
易错点
导后的函数不会变形为
正确答案
3;
解析
(Ⅱ)


令

又



当


∴

考查方向
解题思路
先分离参数后变为

易错点
无
正确答案
(3)略
解析
(Ⅲ)由(Ⅱ)知

令
∴
∴
考查方向
解题思路
根据第(2)问放缩
易错点
不会利用放缩法得到
已知函数
25.若曲线

26.对任意的



正确答案
递增区间为(0,1),(2a+1,+
解析

若曲线
则

则由f

∴f(x)的单调递增区间为(0,1),(2a+1,+
考查方向
解题思路
通过求导,将单调递减区间转成导数正负问题;
易错点
存在性与恒成立的区别
正确答案
解析
∵

不妨设1≤x1<x2≤2,则f(x1)>f(x2),
∴原不等式即为:f(x1)-f(x2)<
即


令g(x)=f(x)-



∴g(x)=f(x)-
∴


而
化简得
即

∵


即

令


∴
则


考查方向
解题思路
本题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值等情况. 本题对考生的逻辑推理与运算求解能力有较高要求.
易错点
构造函数,及讨论问题的全面性。处理逻辑推理与运算求解能力方面易出错。思路不清晰,步骤不严谨
若定义在R上的减函数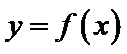
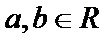
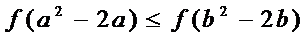
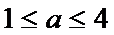
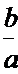
正确答案
解析
由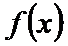
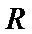
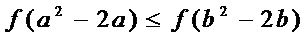
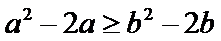
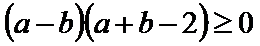
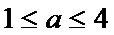
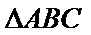
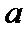
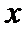
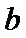
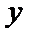
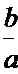
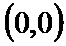
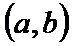
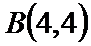
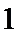
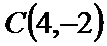
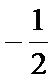
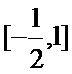
考查方向
解题思路
由函数的单调性结合不等式得出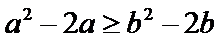
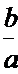
易错点
本题易在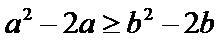
知识点
12.已知



正确答案
知识点
设等差数列{



(1)求数列{
(2)设数列{






正确答案
(1)
(2)
解析
(1)解:设等差数列{


因为已知
可得
整理得,
又因为
当
即,
①②联立可得
由于
所以,
(2)解:由(Ⅰ)可得
将

当
当

①-②可得
所以

两式相减得

所以
知识点
影响基金类产品收益的因素有两方面,其中来自基金自身的因素有( )。
A.货币市场工具
B.基金管理公司的整体业务运行情况
C.基金管理人员的业务素质
D.股票和债券
E.基金管理公司的资产管理与投资策略
正确答案
B,C,E
解析
[解析] 选项AD是来自基金基础市场的因素,所以不选。
某工厂生产某种产品,每日的成本C(单位:元)与日产里x(单位:吨)满足函数关系式C=3+x,每日的销售额R(单位:元)与日产量x满足函数关系式
(1)求k的值;
(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
见解析。
解析
解:(1)由题意可得:L=
因为x=2时,L=3
所以3=2×2+
所以k=18
(2)当0<x<6时,L=2x+
所以L=2(x﹣8)+


当且仅当2(8﹣x)=
当x≥6时,L=11﹣x≤5
所以当x=5时,L取得最大值6
所以当日产量为5吨时,毎日的利润可以达到最大值6。
知识点
设变量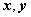
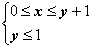
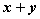
正确答案
解析
略
知识点
已知两条直线










正确答案
解析
在同一坐标系中作出y=m,y=

由




依照题意得


知识点
已知数列



(1)若数列


(2)证明:
正确答案
见解析
解析
(1)解:


证法一:


②-①,得
③-④,得
即

证法二:同证法一,得
令
设
(1)当
(2)假设当

这就是说,当
根据(1)和(2),可知


(2)证明:
知识点
20.甲、乙两公司同时开发同一种新产品,经测算,对于函数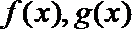
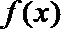
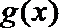
(1)试解释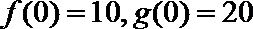
(2)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析