- 不等式
- 共1358题
若a=
正确答案
解析
a=
所以b＜c＜a；
故选：C.
知识点
1.下列关于不等式的说法正确的是（ ）
A任意实数a,b，都有
B任意实数x，
C不等式
D不等式
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确，因为a、b不一定是正实数；C中一元二次方程的根是1+a和1-a，但是当
知识点
14.若
正确答案
2014
解析
x＞0时，因为
知识点
已知定义在（0，+∞）上的函数f（x）=x2+
（1）求a的值；
（2）求不等式|x﹣a|+|x+1|≤4的解集。
正确答案
见解析。
解析
（1）因为a＞0，x＞0，得到x2+
（2）原不等式等价于
（1）因为a＞0，x＞0，根据三个正数的算术﹣几何平均不等式，得
f（x）=x2+
又因为函数f（x）的最小值为3，所以3
解得：a=2。
（2）解法一：由（Ⅰ）得：|x﹣2|+|x+1|≤4。
原不等式等价于
解得﹣
解法二：由（Ⅰ）得：|x﹣2|+|x+1|≤4。
由绝对值的几何意义，可知该不等式即求数轴上到点2和点﹣1的距离之和不大于4的点的集合。
故原不等式解集为{x|﹣
知识点
15.当x∈R，|x|＜1时，有如下表达式：
1＋x＋x2＋…＋xn＋…＝
两边同时积分得：
从而得到如下等式：
请根据以上材料所蕴含的数学思想方法，计算：
正确答案
解析
由
知识点
7.某校为了解本校高三学生学习心里状态，采用系统抽样方法从800人中抽取40人参加某种测试，为此将题目随机编号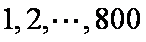
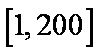
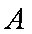
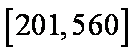
正确答案
解析
略。
知识点
13.若
正确答案
2014
解析
x＞0时，因为
知识点
6.已知x、y满足约束条件
A
B
C
D
正确答案
解析
先画出可以确定的可行域，再根据含参数a的直线过定点（0,3），考虑该直线与直线x＝1交于点
知识点
3.下列关于不等式的说法正确的是( )
A任意实数a,b，都有
B任意实数x，
C不等式
D不等式
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确，因为a、b不一定是正实数；C中一元二次方程的根是1+a和1-a，但是当
知识点
9.不等式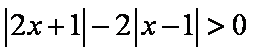
正确答案
1
解析
略。
知识点
2.全集
A
B
C
D
正确答案
解析
知识点
18.设
（1）记使得“
（2）设
正确答案
见解析。
解析
（1）由
（2）由于
所以
知识点
已知
（1） 当a=1时求不等式
（2） 如果函数y=
正确答案
见解析。
解析
（1）f（x）=|2x-1|+x-5=
∴f（x）=|2x-1|+x-5≥0：化为
解得：{x|x≥2或x≤-4}．
（2）
由f（x）=0得，|2x-1|=-ax+5．
令y=|2x-1|，y=-ax+5，作出它们的图象，可以知道，当-2＜a＜2时，这两个函数的图象有两个不同的交点，所以，函数y=f（x）有两个不同的零点．
知识点
5.将甲、乙、丙等六人分配到高中三个年级，每个年级2人，要求甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排种数为 ( )
正确答案
解析
可以先排高三年级有
知识点
6.图是一容量为
正确答案
解析
根据中位数左右两侧的面积相等，也就是概率相等所以中位数为12,第一块的面积为
知识点
扫码查看完整答案与解析