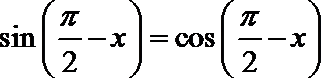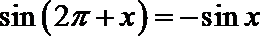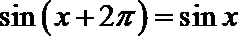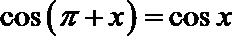- 不等式
- 共1358题
13.已知直线


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果直线y=kx+1与圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若
正确答案
m≥5
解析
解析已在路上飞奔,马上就到!
知识点
2.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设两个正态分布N(μ1,σ12)(σ1>0)和N(μ2,σ22)(σ2>0)曲线如图所示,则有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知不等式组




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.对于数集







(Ⅰ)若

(Ⅱ)若X具有性质P,求证:1X,且当

(Ⅲ)若X具有性质P,且


正确答案
(Ⅰ)选取

所以x=2b,从而x=4.
(Ⅱ)证明:取


由



因为-1是X中唯一的负数,
所以

故1
假设


选取



则



若
若

所以x1=1.
(Ⅲ)[解法一]猜测
记
先证明:若

任取






当



因为





从而


假设


则

得





现用数学归纳法证明:
当n=2时,结论显然成立;
假设n=k时,

当n=k+1时,若
也有性质P,所以
取



若
所以



综上所述,
[解法二]设



记
原点对称.
注意到-1是X中的唯一负数,
所以
由于
……
注意到


解析
解析已在路上飞奔,马上就到!
知识点
13.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列等式中,成立的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2:1,则称此椭圆或双曲线存在“F点”,下列曲线中存在“F点”的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析